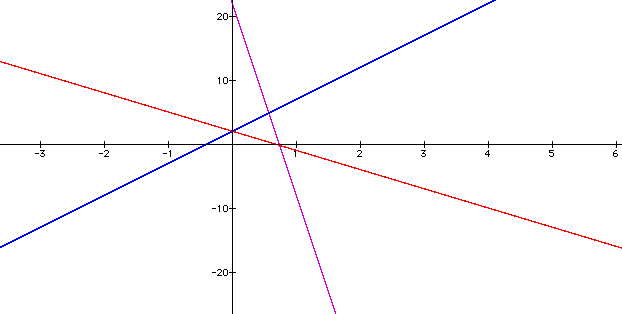
In this investigation we will look at f(x) = 5x+2 and g(x) = -6x+4.
So, when h(x) represents the sum of f(x) and g(x),
For h(x), the product of f(x) and g(x)
The quotient is
Finally, the composite of f(x) and g(x) is
Examining the mulitple functions h(x) leads to the discovery that the product and the composite have the same leading coeffient. This is true for all linear functions f(x) and g(x).
f(x), g(x) and h(x) where h(x) is the sum of f(x) and g(x)
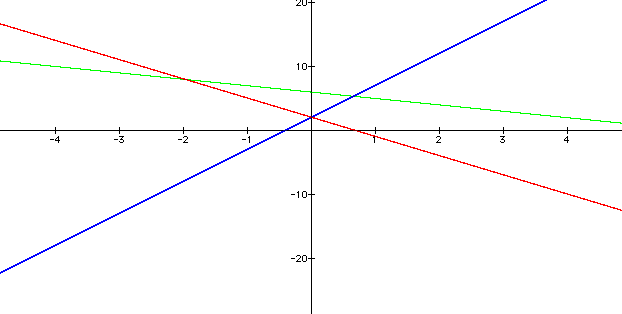
f(x), g(x) and h(x) where h(x) is the product of f(x) and g(x)
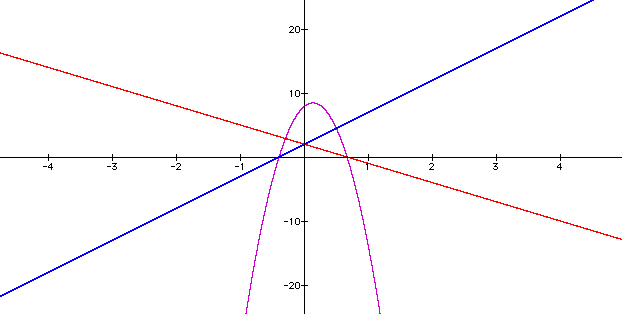
f(x), g(x) and h(x) where h(x) is the quotient of f(x) and g(x)
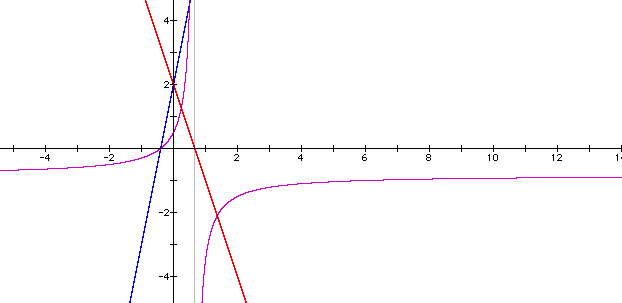
f(x), g(x) and h(x) where h(x) is the composite of f(x) and g(x)