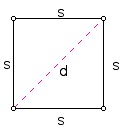
Let's look at the general case of a square to learn about 45-45-90 triangles.

From the Pythagoren Theorem,
![]()
![]()
And from this it proves our
theorem, that in a 45-45-90 triangle, the hypotenuse is ![]() times as long as a leg.
times as long as a leg.
Example:
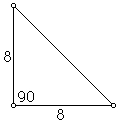 What
is the length of our hypotenuse? According to our theorem the
hypotenuse is square root 2 times as long as a leg. So our hypotenuse
is
What
is the length of our hypotenuse? According to our theorem the
hypotenuse is square root 2 times as long as a leg. So our hypotenuse
is ![]() or about 11.3.
or about 11.3.
For a great 45-45-90 exercise
of a baseball diamond click
here.
There is a special relationship in a 30-60-90 triangle also.
If we draw an altitude from any vertex of an equilateral triangle, the triangle is then seperated into two congruent 30-60-90 triangles. Using the Pythagorean Theorem, it is possible to derive a formula relating the lengths of the sides to each other.
Let s = the measure of a side
Let a = the measure of the altitude
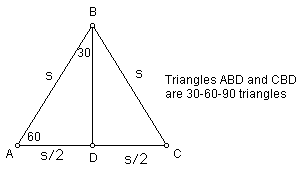

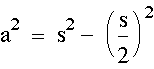
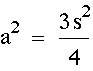
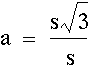
So we can see that in the 30-60-90 triangle, the hypotenuse is twice as long as the shorter leg and the longer leg is suare root of 3 times as long as the shorter leg.