
Iwant to investigate what happens to the graph of
for when a=b, a=0 and b varies, and replacing cos with sin.
Let's look at the graph of the function when a = b =1 and k =1

This is a graph of r = 1+ cos t.
Looking at the graphs of when a = b=1 and k varies. Therefore k is the variable under observation. Looking at the graphs we see a strange happening that I want to generalize below:
As k vaires, the graph of r = 1 +cos Kt changes too. The graph takes on the form of what is called a leaf-rose graph. the number of leaves in these graphs is equivalent to k. Therefore if we set k = 7 then there will be seven leaves.
I wonder what would happen if I were to replace cos () with sin (). I want to graph the equation r= b sin kt. The purposes of having only one variable in the equation, I will set b = k = 1.
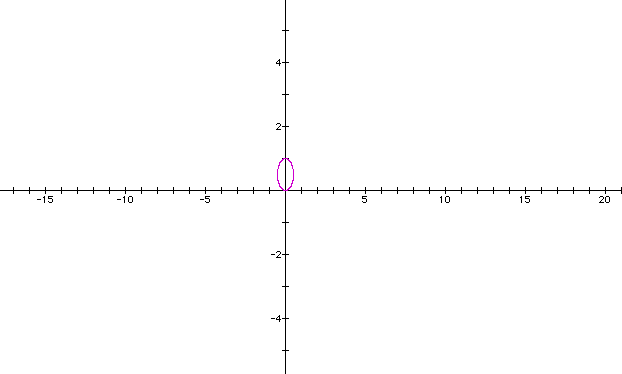
What about when b=k =2.
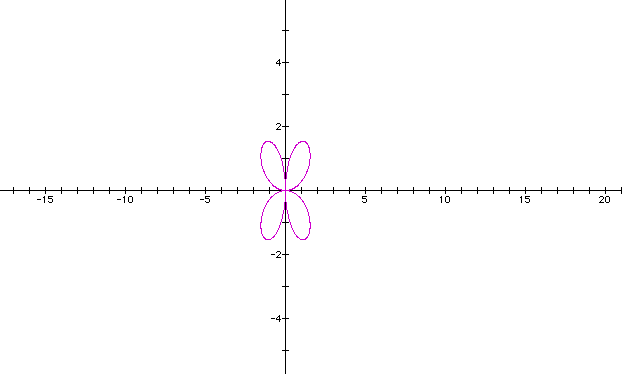
I do not see any obvious patterns forming yet. Do you?