Content:
Parabolic Section-Vertex of a Parabolic Section
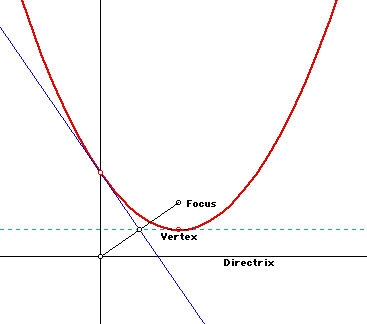
The parabola is the locus of a set of points equidistant from a fixed point, the Focus, and a fixed line, the directrix.

One of the basic properties of parabola is the following:
Property-I: For every point P on the parabola,
|
|
|
Proof: In the first case (FS < PR), since FP = PR and FV = VS =a (by the definition of parabola), PQ = FP - 2a. By Pythegorean Thm applied to the right triangle FPQ,
The second case (FS > PR) is similar...
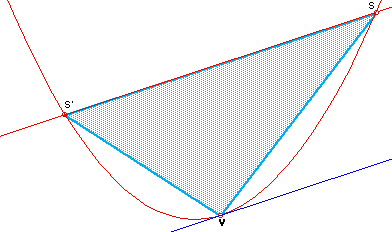
Parabolic Section and Vetex of the Parabolic Section
Consider a parabola, cut it with any straight line, and let S and S' be the points of intersection. For some point V on the parabola, the tangent line at V is parallel to the cut SS'. The parabolic region SVS' is called a parabolic section and V is the vertex of the parabolic section.
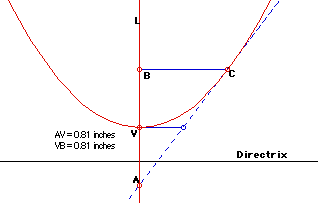
Proposition-I: Let V be the vertex of a parabola. And let the line L be perpendicular to the directrix of the parabola at V. For a point A on L, if AC is constructed, where IAVI = IBVI, then AC is tangent to the parabola (See the figure below)
Proof:

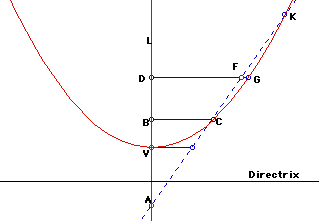
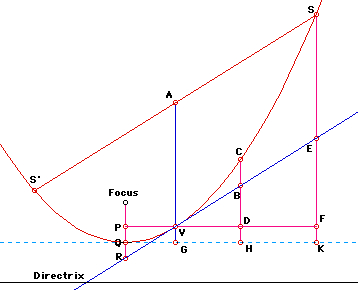
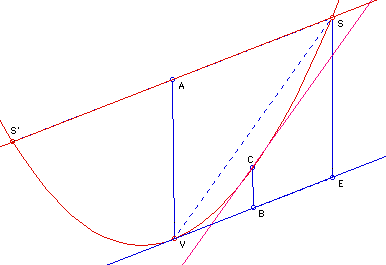
Proposition-II: Let A be the midpoint of the segment SS'. And let E be the feet of the parallel from S on the tangent line at V to AV. Take B on the segment VE . Construct C , which is the intersection point of the parabola and the line passing through B and parallel to AV. Then
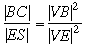
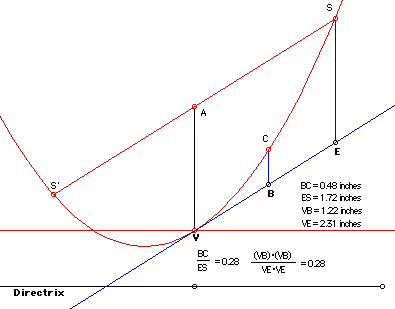
Proof:

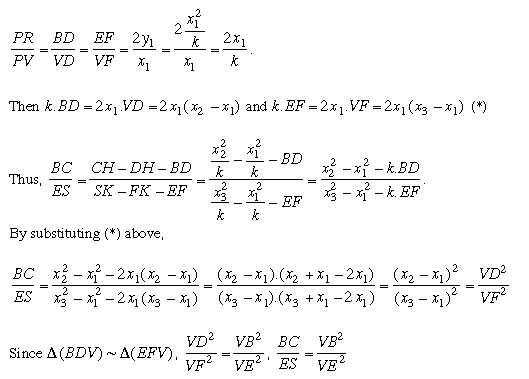
Proposition-III: Let A be the midpoint of the segment SS'. And let E be the feet of the parallel from S on the tangent line at V to AV. Take B as the mid-point of the segment VE . Then C , which is the intersection point of the parabola and the line passing through B and parallel to AV, is the vertex of the parabolic section SVC (See the figure below).
Proof:
