Platonic
Solids
Cont...
Now that you have filled out the chart
on the previous page, let's explore a couple of formulas which may stream
line the process of counting faces, edges, and vertices.
In the first formula, we will allow
V
to be total number of vertices of the solid. F to be the number
of faces, J to be the number of vertices of each face, and L
represents the number of faces at each vertex.
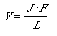
Notice that with a tetrahedron, there
are 4 faces, 3 faces at each vertex, and each face has 3 vertices associated
with it. Therefore, F = 4, J = 3, and L = 3. 
According to our formula, we find that
the total number of vertices of a tetrahedron can be found with:
V=(3*4)/3 = 4
Therefore, a tetrahedron has 4 vertices.
If there is a nice way to calculate
the number of vertices that our solids have, maybe there is a nice way
to calculate the number of edges our figures have. This is my challenge
to you.
-
Derive a formula which will find the number of edges of a
polyhedron of the type we have explored in this unit.
(Hint: Use the previous formula to help you.)
Write your answer on a piece of paper.
Justify why your formula works, and provide an example to show that it
does work. Turn this paper into your teacher when you have completed
this part of the assignment. The correct answer will be provided
to the class at a later date.
![]()
![]()
