Six equilateral triangles with the same vertex are
in the same plane and cannot be "folded" to form a convex 3-dimensional
corner. So, the sum of the measures of the angles of the faces
at one vertex of a regular solid must be less than 360.
Example: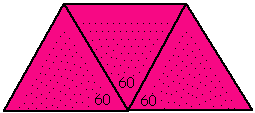 
This figure can be folded to form 3 faces of a tetrahedron. Sum of
the angle measures is less than 360.
Example: 
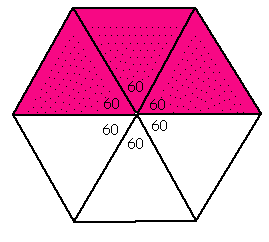This
figure cannot be folded. The sum of the angles is 360.