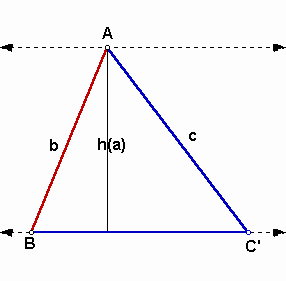
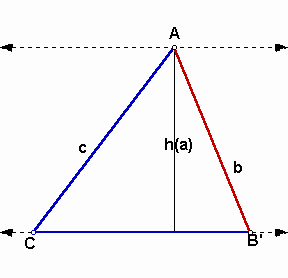
Notation:
The angles at vertices A, B, and C: A, B, and C, respectively
The sides of the triangle opposite vertices A, B, and C: a, b, and c, respectively
The medians: m(a), m(b), m(c)
The altitude: h(a), h(b), h(c)
The segments along an angle bisector to the opposite side: d(a), d(b), d(c)
The radius of the circumcircle: R
The radius of the incircle: r
A way of Construction:
1) center A:
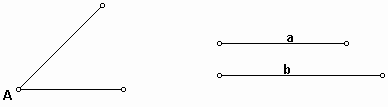
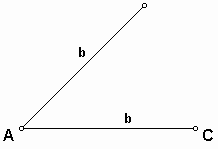
First, copy the segment of length b (segment AC).
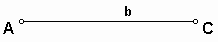
Rotate the segment AC with the center point A and angle A given.
Construct a circle at point A with radius of the length a, i.e. segment BC.
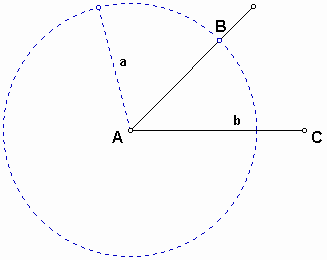
We can have the point B from the previous construction of a circle. B is located on the intersection point of the circle and the segment resulted from the rotation.
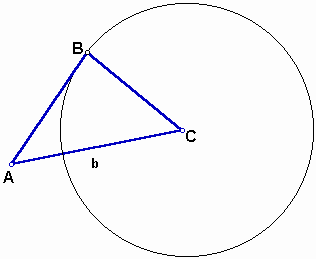
Now, draw a line from the point B to the point C.
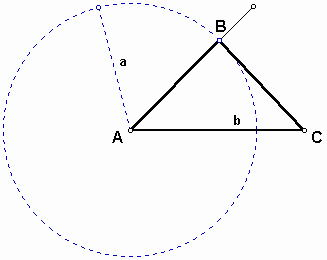
Then we get a triangle of given conditions:
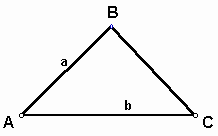
2) center C:
Draw a circle with the center C and radius a.
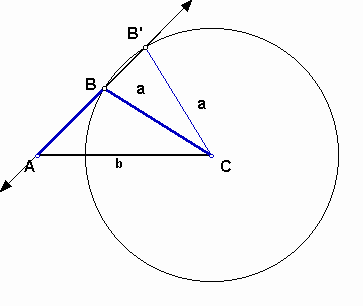
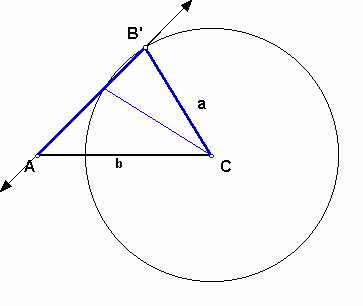
If B = B', that is there is only one point, the triangle becomes right triangle.
GSP Sketch (contri2.gsp)
GSP Script (scontri2.gss)
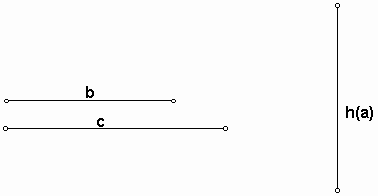
A way of Construction:
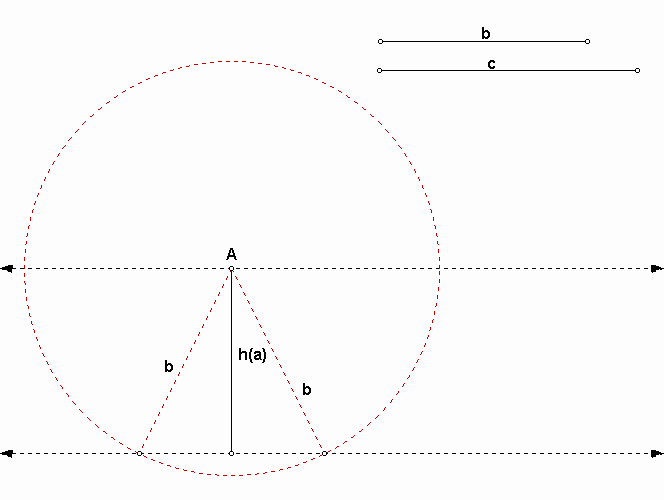
Begin with copying h(a) and construct two parallel lines at both end points of h(a). Take A at one point of end points.
Draw a circle with center A and radius b.
Construct another circle centered A and radius c and mark the intersection points.
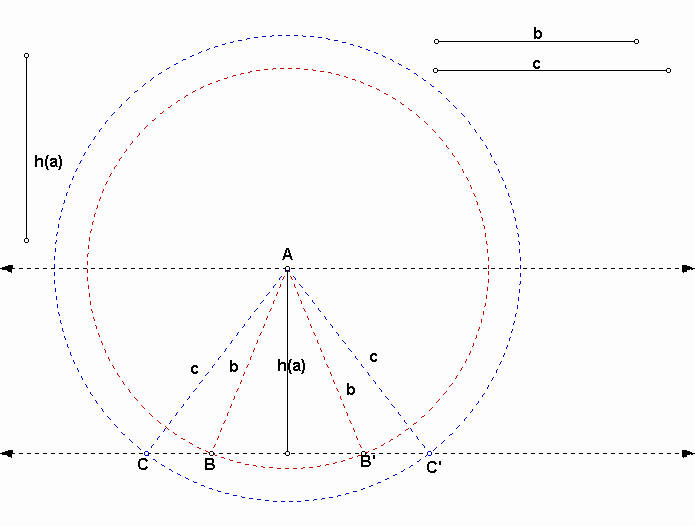
Then you have two possible triangles ABC' and AB'C.