---

Proof of Triangle Side Ratios

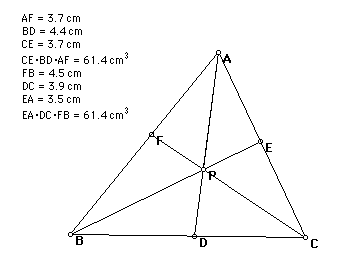
The ratio (CE)(AF)(BD)/(EA)(FB)(DC) = 1. The proof of this involves the construction of parallel lines to create similar triangles as shown below.

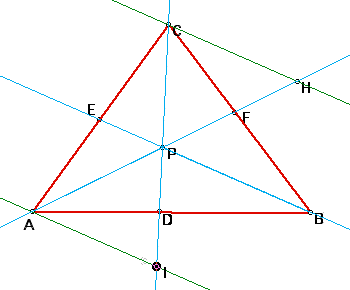
Angle ECP is equal to angle ACI because angle measure depends on rays. Angle CEP is equal to angle CAI by the Transversal Theorem because AI is parallel to EP. Therefore, by Angle-Angle Similarity, triangle ECP is similar to triangle ACI. By the definition of similar, CE/CA = EP/AI.

Angle AEP is equal to angle ACH by the Transversal Theorem. Also, angle EAP is equal to angle CAH because angle measure depends on rays. Therefore, by Angle-Angle Similarity, triangle AEP is similar to triangle ACH. By the definition of similar, AE/AC = EP/CH.

Alternate Interior angles demonstrates that angle PBF is equal to angle HCF and angle BPF is equal to angle CHF. So, by Angle-Angle Similarity triangle PFB is similar to triangle HFC. Using the same logic, it can be said that triangle ADI is similar to triangle BDP.

By the definition of similar, PB/CH = BF/FC and AI/PB = DA/DB.

Using the first two similarity rations, CE = (EP)(AC)/(AI) and AE = (EP)(AC)/(CH). Therefore, CE/EA = CH/AI. The ratio (CE)(AD)(BF)/(EA)(DB)(FC) = [CE/EA]*[AD/DB]*[BF/FC] = [CH/AI]*[AI/PB]*[PB/CH] = 1. Thus, the proof of the ratio is complete, so (CE)(AD)(BF) = (EA)(DB)(FC).