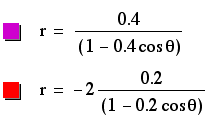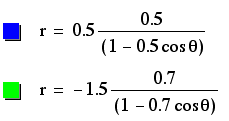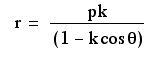
When k =1, this equation forms a parabola turned on its side. If p is negative, it opens to the left, while if p is positive it opens to the right. The magnitude of p determines the amount of stretch in the graph. As p increases, the parabola becomes wider. P also influences the placement of the vertex. For these parabolas, the vertex is always located on the x-axis, but this x-value depends on p. The vertex appears to be located at the point (-p, 0), but closer examination shows that this is not true. (For example, the vertex of the red parabola, where p=2, is not located at (-2,0). The vertex is, however, located at a point with a sign opposite to the sign of p, so as p approahes 0, the vertex approaches (-p, 0).
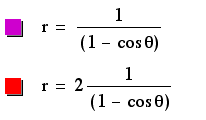
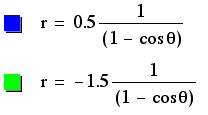
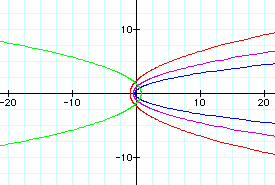
When k >1, the graphs become hyperboles. These hyperboles open to the left and right, similar to the parabolas in the above example. P again denotes the amount of stretch, with equations containing a greater p having a wider graph than equations containing a lesser p. The only graph with a negative p in this example is the only graph located to the right of the y-axis. Therefore, the sign of p determines the placement of the graph. Again, the vertex is located on the x-axis with an x-coordinate that is the opposite sign from p, if we consider the vertex to be the point of intersection of the assymptotes. Even if we consider these graphs to have two vertices, one for each component side of the hyperbole, both of these vertices are still located on part of the x-axis with the opposite sign of p.
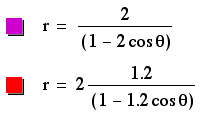
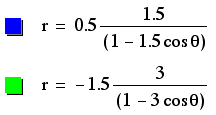
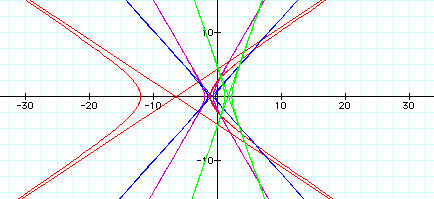
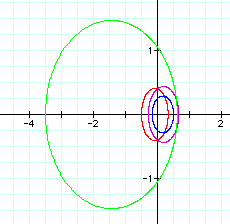
When k <1, these graphs become ellipses. The values of p and k determine the heighth and width of these ellipses. The sign of p determines the location of the center. If p is negative, the center is located to the left of the y-axis, while if p is positive, the center is located to the right of the y-axis. the centers are located on the x-axis, as were the vertices of the parabolas and hyperboles.