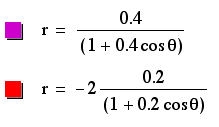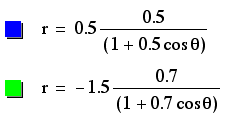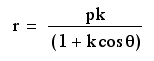
These equations form parabolas. When p is negative, the parabola has a vertex with a negative x-coordinate and opens to the right. When p is positive, the parabola has a vertex with a positive x-coordinate and opens to the left. The vertex is always located along the x-axis, which means that the y-coordinate for the vertex is 0. The value of p determines the amount of stretch, meaning that a smaller p implies a smaller width of the graph, and a larger p implies a larger width of the graph.

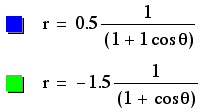
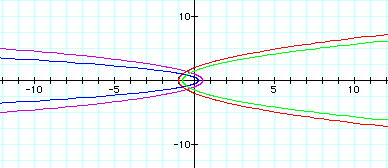
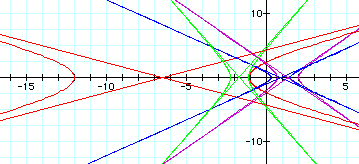
The vertices and width of these hyperboles are determined by the values of p and k. A negative p yields a vertex or vertices to the left of the y-axis, while a positive p yields a vertex or vertices to the right of the y-axis. The width (or stretch) of the hyperbole is determined by a combination of the k and p values.
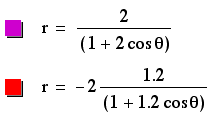
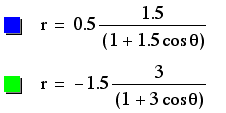
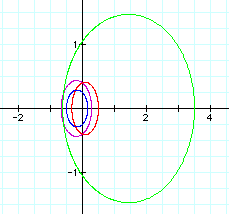
The centers of the ellipses created by these graphs are determined in an opposite manner to the vertices of the hyperboles above. If p is negative, the x-coordinate of the center is positive. If p is positive, the x-coordinate of the center is negative. Again, the centers are always located on the x-axis, so the y-coordinates are always 0. The width and heighth of these ellipses are determined again by p and k. The equation with a p-value of -1.5 is the widest and tallest, while the equation with the p-value of 0.5 combined with a low k-value is the smallest in width and heighth. Therefore, as p increases, the area increases, and the same occurs with k.