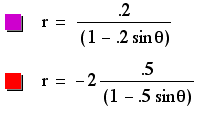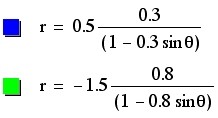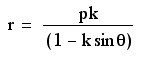
The graphs formed by various values of p when k = 1 are parabolas. When p is negative, they open down. When p is positive, the graphs open up. P also affects the stretch of the graph. A large p causes the graph to open wider and therefore be more "stretched out". The vertex of the parabola is also affected by p. A negative p yields a positive vertex while a positive p yields a negative vertex.
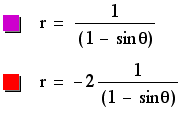
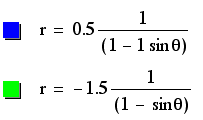
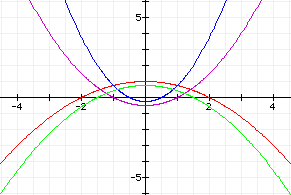
Changing the k to be great than one has an immense impect on the graphs produced. These are now hyperbolas with included assymptotes. The "parabola-like" parts of the graphs are farther apart when p and k are small. If we call the vertex the intersection of the assymptotes, the vertex has the opposite sign to p. The exact location of the vertex, however, depends upon both p and k. Again, the amount of "stretch" is determined by a combination of p and k. This combination effect cannot be produced by simply the product of p and k, so it must therefore be determined by an intricate relationship, but it appears that similar values of p and k interact to form a strong effect while dissimilar values cancel each other out and do not affect the generic graph as much.
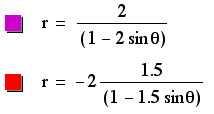
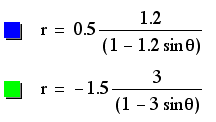
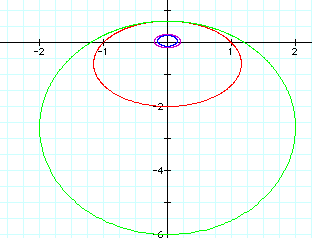
The ellipses formed from these equations all include the origin in their interiors. K appears to have a stronger effect on these graphs than p because when p is negative, the larger value of k causes a larger circle, regardless of the magnitude of p. When p is positive, the opposite appears to happen. It can be noted that the graphs with negative p-values intersect on the y-axis, as do the graphs with positive p-values. This demonstrates that instead of simply growing larger from the center out, these graphs grow larger from one side. The other side (or in this case the top) remains constant as the ellipses expand. The vertices are positive for all of the ellipses, but this could be caused by the fact that k is positive. This conclusion, however, mightn ot be valid becuase in past examples, the vertex did not depend on the sign of k. Perhaps these graphs actually do always have positive centers.