

This investigation involves the construction of circles which are tangent to a pair of given circles. For example, look at the two circles below. It is possible to construct a third circle that is tangent to both of the given circles.

Pick an arbitrary point on the circle with center at A and construct a line through this point and A.

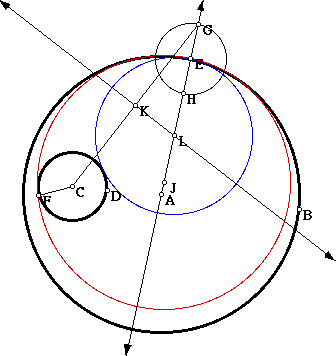
Now construct a circle with a radius equal to the radius of circle C with point E as a center and mark the intersections of the circle with the line.

Construct a segment from C to the point H of intersection of the circle with the line and then construct the perpendicular bisector of the segment and find its intersection with the line through A.

This new point, J, is the center of a circle that is tangent to our given circles. Draw a circle using J as the center and JE as the radius.

As you can see, the red circle indeed is tangent to both of our given circles. Using point G and the center C, it is also possible to draw another circle tangent to both of our given circles.
You could have constructed a similar pair of tangent circles using the other point of intersection.

The location of the four tangent circles was strictly dependent upon our choice of a line through the center of the large circle. This leads us to conjecture that there are in fact an infinite number of circles that are tangent to our given circles. We can demonstrate this through the use of animation. If you would like to see an animation of one of the tangent circles as the point E is moved along circle C click here.
This animation is an informal proof that an infinite number of tangent circles exist to the given circle.
Now that we have the four tangent circles, let's see what happens as we move the smaller circle toward the larger circle. As the circles become tangent we get the following picture.

As some expected, the two outer tangent circles become coincident with the larger of our two circles. Now what happens as the smaller circle is intersected by the larger circle?

The outer tangent circles are now both outside the larger circle. Of course, we should have expected this since the circles can only be tangent to both circles if they do not intersect one of the circles. To do this, they must be outside of both circles. Now, what happens to the blue inner tangent circles as the smaller circle again approaches tangency?

Now the blue circles are coincident with the larger circle. Finally, what happens as the circles become disjoint?

Now all four tangent circles have moved outside of the larger circle. (I have zoomed out to show all of the picture.). However, now we don't seem to have all the possible cases for tangent circles. Something seems to be missing. The larger circle is within all of these tangent circles. Is there a tangent circle that does not contain the larger circle? Is there a tangent circle that does not contain either circle? The answer to both these questions is yes. Futher exploration involving the postion of the line used to construct the four tangent circles reveals that there are four basic families of tangent circles that occur when our circles are disjoint.

One family of tangent circles contains both of our original circles. The second family of tangent circles contains the larger circle but not the smaller. The third family of tangent circles (which is related to the second in some way) contains the smaller circle but not the larger. Finally, the fourth family of tangent circles contains neither circle. If the line that was used to construct these families of tangent circles is repositioned so that the angle with respect to the line connecting the centers of the original two circles is increased , the light blue tangent circle is most affected at first. It gradually grows larger as its center moves further away and at a critical point the center flips and the light blue circle becomes a member of one of the other tangent circles.

Notice that the light blue circle now is one of the family of tangent cirlces that contains the larger circle. What happens as we increase the angle some more. From looking at the picture above we expect that the dark blue tangent circle will be the next to be affected in some way. Let's see.

So the dark blue tangent circle becomes a member of the family of tangent circles that contains both of the original circles. To see what happens as the line is rotated about the center C of the larger circle click here.
This was a very interesting investigation. The most interesting part was when I started trying to find all of the possible cases for tangent circles when the original circles are disjoint. That is when I started moving the line used to construct the tangent circles and discovered its influence on the types and positions of the tangent circles. There is further exploration which I did but is not included that involves the construction of up to 10 related families of tangent circles. The four above and four more that are complementary and two more that are based upon the perpendicular bisector of the two tangent lines from A to a circle with the same radius constructed within circle C.