Rates

Introduction

The development of calculus was motivated by the study of motion. One of the characteristics of motion is velocity, or directed rate of change in distance per unit of time. The concept of velocity has analogs in other parts of science and engineering. One of these, work, will be used along with time and distance, in this lesson.

Time and Distance

The components of time and distance studies are: acceleration, velocity and distance. The equations for these components are given below as functions of time.

Acceleration:

Velocity (speed):

Distance:

The assumption has been made that acceleration is a linear function. This is most likely not true.

Example:

Use this example to model the use of the functions for time and distance.

Suppose you have experimented and you have determined that your car has an acceleration function a = -0.1t + 16 ft/sec² at full throttle starting from a standstill. Find the time it would take your car to travel a distance of a quarter mile and the velocity at that time.

Solution:

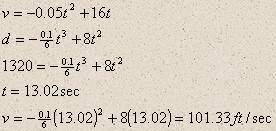
The roots to the distance equation were found by using the polynomial solver on a TI 85 calculator. There were, of course three roots, however; only the one listed seemed reasonable. I recommend that your students should be using a TI 85 or TI 86 calculator. If so, have them use the polynomial solver and find the three roots for themselves. Then discuss the reasonableness of each root. It would also help to graph the polynomial on their calculators. The graph is shown below.

Work

The components of the study of work are time, mass, acceleration, power, force, distance, and energy (work). Notice that the study of work has many of the same components as the study of motion. Mass is a constant associated with an object. Some times mass is incorrectly referred to as weight. Weight is really a measure of force. The weight of an object is its mass multiplied by the standard unit of gravity, which is a measure of the acceleration of any object at the earth’s surface. Using the equation for acceleration from the time and distance equations we have the following:

Force:

Work:

Power:

The work equation above is very general. Actually all of the equations above are very general. For illustration purposes acceleration is usually considered to be a constant. That greatly simplifies the equations above. They become:

Force:

Work:

Power:

Example:

An automobile weighing 3500 pounds is subjected to a constant acceleration of 10 ft/sec². If the car starts from a standstill, how much work in pounds-feet will it take to accelerate the car to 60 mph?

Assign the above problem for the students to do as seatwork. Circulate among the students to provide any necessary guidance.

Solution:

In Lesson 2 we will discuss average velocity and average power. Make appropriate comments to the students to prepare them for this.

RETURN