Introduction

In Lesson 3 we introduced the concept of instantaneous rate of change. In this lesson we will extend that concept to define the derivative. We will introduce the formal definition of the derivative and demonstrate the concept of the derivative using GSP.

The Slope of the Tangent Line at a Point

In the previous lesson we investigated the difference quotient and its meaning when applied to a function. We saw that when the difference between t and c in the difference quotient approaches zero, the secant line becomes the tangent to the curve of the function at t = c. We also observed that the tangent to the curve at a point is the instantaneous rate of change, or instantaneous slope, of the function at that point. Let’s formalize this concept. Rewrite the difference quotient as

Now we can define the slope of the tangent line at any value of the independent variable x of a function as

Example: Find the slope of the tangent line to y = 3x² at (1,3).

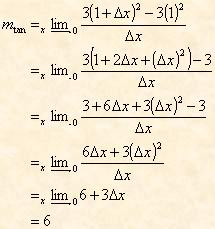
The Derivative

What we actually have done is to define the derivative of a function. The derivative is defined as:

Let’s choose a function and experiment using GSP to help us visualize what is going on as Dx goes to zero. I have graphed the function y = -4x². The graph appears below.

Link to the GSP sketch by clicking here and drag point C back and forth along the x-axis and observe the slope of the equation of the line. As C approaches 0.5 from either side of 0.5 the slope seems to approach 4. Is this correct? The coordinates of point E are (0.5,1). Using the definition of the derivative given above we have:

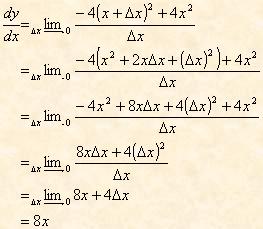
So the slope at any point on the curve is 8x. Then at x = 0.5, the slope would be 4 as we supposed from the GSP sketch.

We have used the notation dy/dx here to denote the derivative. Now would be a good time to introduce other notations for the derivative to the students, such as f’(x) or y’.

Now we will revisit the functions used in the previous lesson and use the GSP sketches and the definition of the derivative to reinforce this concept. Afterwards we will work out several examples both on the board and as seatwork.

RETURN