Introduction

In this lesson we introduce the derivative of the product of two functions. We begin by providing a motivation through a seatwork problem and then introduce the product rule.

Motivation

Have the students calculate the derivative of the following at their seats. They may do the calculation using the tools already introduced for calculating derivatives, including the definition, if they wish.

y = (3x³ – 1)(2x-1)

Most students will do the multiplication and then treat the result as a polynomial, which isn’t too tedious. Some students will try to use the difference quotient, which is very tedious. Everyone should get the result, dy/dx = 24x³ –9x² –2. Now is the time to introduce the product rule.

The Product Rule

If y = f (x) can be written as the product of two functions u = g(x) and v = h(x) then

y = uv.

The derivative dy/dx of y can be found as

Using the example from the previous paragraph,

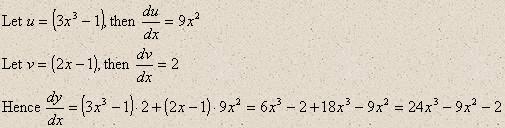
Now work several more examples for the students and have them work several examples at the board and at their seats while you observe and coach. The product rule is presented here without proof. This was done because the intended student audience was not anticipated to go beyond a two-semester course in calculus in their studies. At the institution where the author teaches, this is the highest-level mathematics course taught.

RETURN