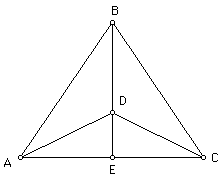
Problem:
Given a triangle ABC, find a point D such that segments AD, BD, and CD trisect the area of the triangle into three regions with equal area.
Define D and prove that the triangle is divided into three regions with equal area. Provide a construction for D.
Exploration:
We know that the area of triangle ABC is 1/2*BASE*HEIGHT.
We also know that the area of ADC is going to be 1/3*1/2*BASE*HEIGHT = 1/6*BASE*HEIGHT, since the area of the three triangles is to be 1/3 the area of the original triangle.
Since the base of triangle ABC and of triangle ADC will be the same, it will suffice to construct the height of triangle ADC to be 1/3 the height of triangle ABC.
Therefore, we need a point D such that DE=1/3*BE. This will cover the case when the height of triangle ABC is the median, segment BE.

We also need to consider the case when the height of triangle ABC is not the median.
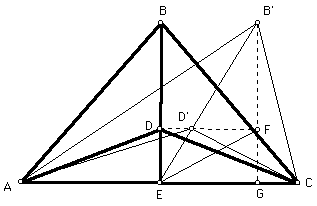
In this case, let's look at triangle AB'C. The height of triangle AB'C is not the median, segment B'E, but it is segment B'G. If we know that point F is a point such that FG=1/3*B'G, then the area of triangle AD'C will be one-third the area of triangle AB'C.
What we need to know then is that point D', the centroid of triangle AB'C is a point such that D'E=1/3*B'E. If we can show this, then we can show that point F will satisfy the above criteria so that the area of triangle AD'C is one-third the area of triangle AB'C.
Lemma:
The medians of a triangle concur at a point D that is two-thirds the distance from each vertex to the opposite midpoint.
This point of concurrence is called the centroid. To see the proof of our lemma, click here.
Now that we know this about the centroid, we can show that point F is a point such that FG=1/3*B'G. Let's recall our scenario:
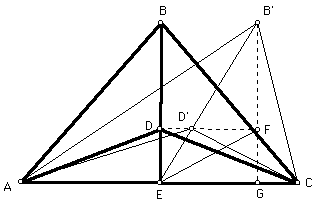
Notice that we have similar triangles in our picture.
Triangle EB'G is similar to triangle D'B'F since angle B'D'F is congruent to angle B'EG, and angle B'FD' is congruent to angle B'GE, and both triangles share angle B'.
Now, since we have similar triangles and we know from our lemma that D'E=1/3*B'E, we also know that FG=1/3*B'G.
Recall from above that this is what we need to make the area of triangle AD'C = one-third the area of trangle AB'C.
Conclusion:
The centroid of any triangle ABC is a point D such that segments AD, BD and CD will trisect the area of triangle ABC.