
To Prove
The bisector of an angle of a triangle divides the opposite side into segments that are proportional to the adjacent sides.

That is, for any triangle ABC, the bisector of the angle at C divides the opposite side into segments of length x and y such that

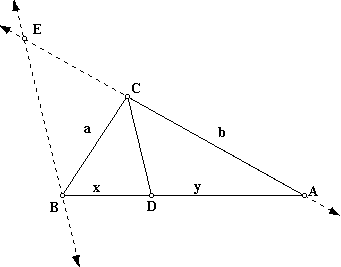
If we draw BE parallel to CD, meeting AC extended to E, then we can notice that triangle ACD is similar to triangle AEB.
We know that these two triangles are similar because they share three congruent angles.
Angle A is congruent to itself.
Angle EBA is congruent to angle CDA because CD is parallel to EB by construction, and they are cut by the transversal AB.
Angle BEA is congruent to angle DCA because CD is parallel to EB by construction, and they are cut by the transversal EA.
Since these two triangles are similar, we know that
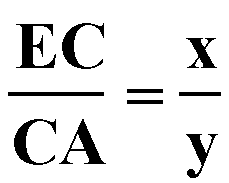
Since the relationship that we are looking for is

and since b is segment CA, what we need is for a to be congruent to EC.
What we can look at is triangle BCE. If a is to be congruent to EC, then triangle BCE will be an isosceles triangle.
Since angle E is congruent to angle DCA, angle EBC must also be congruent to angle DCA.
Let's look at what happens when we draw the parallel line to BA through C.

Notice that FCDB is a parallelogram. This tells us that angle FBC is congruent to angle BCD.
Now, since CD is the angle bisector of angle BCA, angle BCD is congruent to angle DCA.
Therefore, angle FBC (or angle EBC) is congruent to angle DCA.
Recall that angle DCA is congruent to angle E. Therefore, angle EBC is congruent to angle E.
This tells us that triangle BCE is an isosceles triangle, which tells us that a is congruent to EC.
Now, our original relationship of
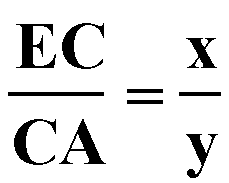
can be rewritten as

and we are done.