The value of t determines a point (x, y) on the coordinate plan. As t varies, the point (x, y) will trace out a curve, called a parametric curve, where t is the parameter.
 |
|
|
.The graph below is for the value of =
. As time t changes, the curve that
is formed is shaped like
a bowtie, going through the origin. There are two loops formed here, crossing the x-axis at (-4, 0) and
(4, 0). The range goes from [-3, 3].
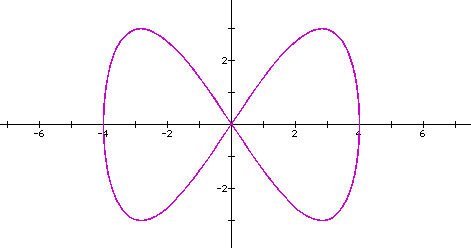
The next graph illustrates what occurs when
= 
. This
graph also goes through the origin and its domain is [-4, 4] and
the range is [-3, 3]. The graph now presents four loops.
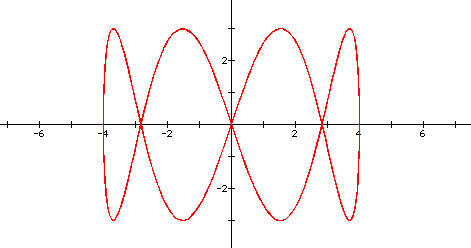
What might you conclude from these two graphs? Click here for a quick summary.
Now for other values of .
The graph shown below is for = 
. Notice here that there are three loops
or three humps and the range for t did have to be increased to
get the complete graph since more curvature is occuring.
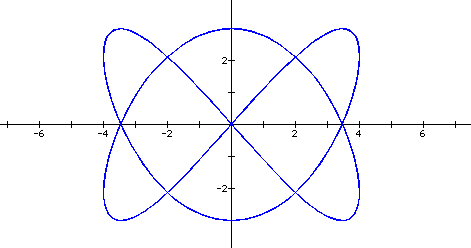
How do you think the graph of =
might look? Click here to see if your guess
if corrrect.
We became curious about some other values of
. The graph =
was somewhat surprising.
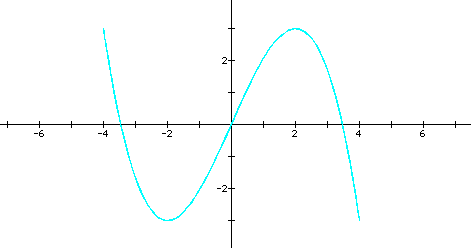
It was not a closed or connected figure. This lead me to the conclusion that is seems as though when
a + b = an odd value, the graph is connected and when a + b = an even value, the graph is not connected.
As a final investigation, we graphed = 
.
It followed the same pattern and is connect since 12 + 13 = 25 is odd and has 13 humps. As the fractions get closer to 1, the curve that is traced out becomes more involved and more elaborate. The path that t follows beomes longer.
Return to Vicki Tarleton's Page