Assignment #2

Horizontal and Vertical Shifts of Parabolas

by

Vicki Tarleton

 Horizontal Shifts

The following will be an exploration of changing to values of d in the equation .

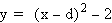The graphs below will show positive and negative values for d.

The following graph illustrates what shifts occur when d = 2, d = 3, d = 5, and d = 7.

 

The next graph displays the shifts for negative values of d, such as d = -2, d = -3, d = -5, and d = -7.

 

One can observe from the above investigations that when a quadratic function is in the form 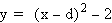, positive values of d cause a horizontal shift of the parabola to the right, the number of

units d. When d is a negative value, the graph will shift horizontally to the left d units.

 Vertical Shifts

As a continuation of this exporation, let's look at the vertical shifts of the quadratic function.

Given the form of a parabola as 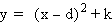, the vertex is (d, k). Let's look at positive and negative values for k. For this exploration h will be zero.

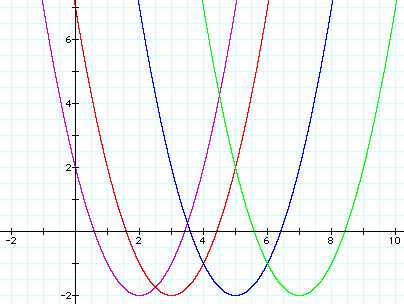
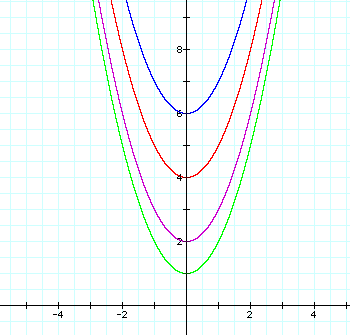
Observe the following shifts for the values k = 1, k = 2, k = 4, k = 6.

Observe the following shifts for the values k = -1, k = -2, k = -4, k = -6.

 

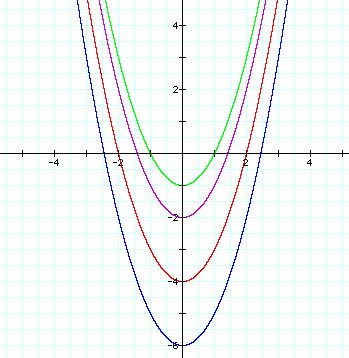
Looking at the exploration given, positive values of k cause a vertical shift up k units. Negative values of k

cause a vertical shift down k units. Therefore, from this we see that the vertex is (d, k) when given the form .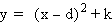

 

Conclusion

Changing the value of d causes a horizontal shift and changing the value of k causes a vertical shift. Changing these values will not cause any change in the shape of the parabola.

What would you expect the graph of 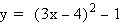to look like?

(Notice the coefficient of x is no longer 1.)

Take a guess and click here to find out if you are right.

Return to Vicki Tarleton's Page