Department of Mathematics Education
Dr. J. Wilson, EMAT 6690

Eudoxus’ Influence on Euclid’s Elements
with a close look at
The Method of Exhaustion
by David Wise

Euclid’s Elements, by far his most famous and important work, is a comprehensive collection of the mathematical knowledge discovered by the classical Greeks, and thus represents a mathematical history of the age just prior to Euclid and the development of a subject, i.e. Euclidean Geometry. There is question as to whether the Elements was meant to be a treatise for mathematics scholars or a text for students (Kline 57). Regardless of the original purpose, the thirteen books that comprise the Elements became the "centre of mathematical teaching for 2000 years" (Euclid of Alexandria 3).

Relatively little is known about the classical period, but historians are certain that Euclid did not discover most of the results in the Elements. However, Euclid’s brilliance as a mathematician is evident in that he chose the axioms, arranged the theorems, and applied a new level of rigor to proofs. It is believed that Euclid acquired a great deal of the material for the Elements from the Platonists, Eudoxus, Theaetetus, and others. In fact, Eudoxus’ work is the basis for Books V and XII of the Elements (Kline 57).

Book V is considered by most authorities to be the greatest achievement of Euclidean Geometry because it extended the Pythagorean theory of proportion. The Pythagorean theory of proportion only dealt with commensurable magnitudes, which are magnitudes whose ratio is restricted to those that can be expressed by a ratio of whole numbers. Euclid relied upon Eudoxus’ work with proportions to develop Book V, which extended the theory of proportions to include incommensurable ratios and still avoided irrational numbers. Book V was crucial in the development of the remaining books of the Elements because it provided the theory for all kinds of magnitudes. In fact, Book V played a key role in the subsequent history of mathematics in that Eudoxus’ theory of proportion required continuous quantities to be treated entirely on a geometric basis. It was not until about 1800 that a theory of rational numbers was developed to provide a foundation for irrational numbers (Kline 69).

In Book XII, Euclid proves eighteen propositions on areas and volumes bounded by curves. Eudoxus’ theory of proportion provides a necessary foundation, but it is Euclid’s use of Eudoxus’ method of exhaustion that is the key element to providing rigorous proofs. The method of exhaustion is a modern term that came into use during the seventeen century and refers to the approximation of a figure using a sequence of inscribed figures within it. The successive inscribed figures "exhaust" the original figure. The important feature of this principle is that the sequence of approximations is made so that the difference between the original figure and the inscribed figure decreases by at least half at each step of the sequence. The method of exhaustion was essential in proving propositions 2, 5, 10, 11, 12, and 18 of Book XII (Kline 83).

Perhaps two of the most easily recognized propositions from Book XII by anyone that has taken high school geometry are propositions 2 and 18:

Proposition 2 is stating that circles are proportional to the squares of their diameters (C1/C2 = (d1)2/(d2)2 ), while proposition 18 is stating that circles are proportional to the cubes of their diameters (C1/C2 = (d1)3/(d2)3 ). While these propositions are routinely shrugged at by our students as being simplistic, known facts, Euclid’s proofs are quite rigorous. High school students can benefit greatly by studying Eudoxus’ method of exhaustion. We will examine the proof of proposition 2 in detail, paying particular attention to the use of the method of exhaustion.

In Heath’s translation of the Elements, Euclid’s proof of proposition 2 is as follows. At the end of each appropriate paragraph, a reference to the proposition(s) used is provided:

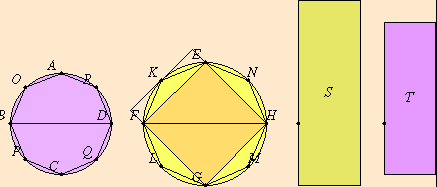
  • "Circles are to one another as the squares on their diameters.


    (diagram provided by Joyce)

     Let ABCD, EFGH be circles, and BD, FH their diameters; I say that, as the circle ABCD is to the circle EFGH, so is the square on BD to the square on FH.

    For, if the square on BD is not to the square on FH as the circle ABCD is to the circle EFGH, then, as the square on BD is to the square on FH, so will the circle ABCD be either to some less area than the circle EFGH, or to a greater.

    First, let it be in that ratio to a less area S.

    Let the square EFGH be inscribed in the circle EFGH; then the inscribed square is greater than the half of the circle EFGH, inasmuch as, if through the points E, F, G, H we draw tangents to the circle, the square EFGH is half the square circumscribed about the circle, and the circle is less than the circumscribed square; hence the inscribed square EFGH is greater than the half of the circle EFGH. [IV. 6 and III. 17]

    Let the circumferences EF, FG, GH, HE be bisected at the points K, L, M, N, and let EK, KF, FL, LG, GM, MH, HN, NE be joined; therefore each of the triangles EKF, FLG, GMH, HNE is also greater than the half of the segment of the circle about it, inasmuch as, if through the points K, L, M, N we draw tangents to the circle and complete the parallelograms on the straight lines EF, FG, GH, HE, each of the triangles EKF, FLG, GMH, HNE will be half of the parallelogram about it, while the segment about it is less than the parallelogram; hence each of the triangles EKF, FLG, GMH, HNE is greater than the half of the segment of the circle about it. [III. 17]

    Thus, by bisecting the remaining circumferences and joining straight lines, and by doing this continually, we shall leave some segments of the circle which will be less than the excess by which the circle EFGH exceeds the area S.

    For it was proved in the first theorem of the tenth book that, if two unequal magnitudes be set out, and if from the greater there be subtracted a magnitude greater than the half, and from that which is left a greater than the half, and if this be done continually, there will be left some magnitude which will be less than the lesser magnitude set out. [X. 1]

    Let segments be left such as described, and let the segments of the circle EFGH on EK, KF, FL, LG, GM, MH, HN, NE be less than the excess by which the circle EFGH exceeds the area S.

    Therefore the remainder, the polygon EKFLGMHN, is greater than the area S.

    Let there be inscribed, also, in the circle ABCD the polygon AOBPCQDR similar to the polygon EKFLGMHN; therefore, as the square on BD is to the square on FH, so is the polygon AOBPCQDR to the polygon EKFLGMHN. [XII. 1]

    But, as the square on BD is to the square on FH, so also is the circle ABCD to the area S; therefore also, as the circle ABCD is to the area S, so is the polygon AOBPCQDR to the polygon EKFLGMHN; therefore, alternately, as the circle ABCD is to the polygon inscribed in it, so is the area S to the polygon EKFLGMHN. [V. 11 and V. 16]

    But the circle ABCD is greater than the polygon inscribed in it; therefore the area S is also greater than the polygon EKFLGMHN.

    But it is also less: which is impossible.

    Therefore, as the square on BD is to the square on FH, so is not the circle ABCD to any area less than the circle EFGH.

    Similarly we can prove that neither is the circle EFGH to any area less than the circle ABCD as the square on FH is to the square on BD.

    I say next that neither is the circle ABCD to any area greater than the circle EFGH as the square on BD is to the square on FH.

    For, if possible, let it be in that ratio to a greater area S.

    Therefore, inversely, as the square on FH is to the square on DB, so is the area S to the circle ABCD.

    But, as the area S is to the circle ABCD, so is the circle EFGH to some area less than the circle ABCD; therefore also, as the square on FH is to the square on BD, so is the circle EFGH to some area less than the circle ABCD: which was proved impossible. [Lemma and V. 11]

    Therefore, as the square on BD is to the square on FH, so is not the circle ABCD to any area greater than the circle EFGH.

    And it was proved that neither is it in that ratio to any area less than the circle EFGH; therefore, as the square on BD is to the square on FH, so is the circle ABCD to the circle EFGH.

    Therefore etc. Q. E. D.

    LEMMA.

    I say that, the area S being greater than the circle EFGH, as the area S is to the circle ABCD, so is the circle EFGH to some area less than the circle ABCD.

    For let it be contrived that, as the area S is to the circle ABCD, so is the circle EFGH to the area T.

    I say that the area T is less than the circle ABCD.

    For since, as the area S is to the circle ABCD, so is the circle EFGH to the area T, therefore, alternately, as the area S is to the circle EFGH, so is the circle ABCD to the area T. [V. 16]

    But the area S is greater than the circle EFGH; therefore the circle ABCD is also greater than the area T.

    Hence, as the area S is to the circle ABCD, so is the circle EFGH to some area less than the circle ABCD. Q. E. D." (Euclid’s Elements 12.2 1).

    • Euclid deals with three cases when comparing the ratio of the squares of BD:FH to the ratio of the circles ABCD:EFGH. The first case is that the ratio of the squares BD:FH equals ABCD:S where S is some area less than circle EFGH. Euclid uses most of the proof to refute this case by employing Eudoxus’ method of exhaustion. In order to approximate the circles by successive inscribed polygons, the square EFGH is inscribed in the circle EFGH, and it is shown that the remainder is less than half the circle. The circumferences are bisected to construct an octagon EKFLGMHN, and again the remainder of the circle is shown to be less than half the previous remainder. This process can be continued as much as one wishes, constructing polygons with 16, 32, 64, etc., sides which increasingly approximate the circumscribed circle. Each successive polygon leaves a remainder less than half of the previous remainder. At some stage of this process, the circle EFGH exceeds the area S by some finite amount, and using proposition X. 1, the remainder will be less than the excess of circle EFGH over S. Euclid uses the octagon EKFLGMHN stage throughout the rest of the proof. More specifically,

    circle EFGH – octagon EKFLGMHN < circle EFGH – area S, therefore

    area S < octagon EKFLGMHN.

    At this step in the proof a similar octagon AOBPCQDR is inscribed in circle ABCD. Thus,

    circle ABCD : area S = (BC)2:(FH)2, and

    (BC)2:(FH)2 = octagon AOBPCQDR : octagon EKFLGMHN, by proposition XII. 1, so

    circle ABCD : octagon AOBPCQDR = area S : octagon EKFLGMHN.

    However, circle ABCD > octagon AOBPCQDR, so

    area S > octagon EKFLGMHN.

    This last statement contradicts the prior statement that area S < octagon EKFLGMHN (Joyce 1).
     
    The second case is that the ratio of the squares BD:FH equals ABCD:S, where S is some area greater than circle EFGH. Euclid inverts this statement to the statement that the ratio of the squares FB:BD equals EFGH to some area less than circle ABCD, which is the first case that has been contradicted. Thus, by proving a contradiction in the first two cases, Euclid proves the third case of the ratios of the squares BD:FH equals the ratio of the circles ABCD:EFGH. As a note, modern mathematicians point out that there is a gap in Euclid’s last step of this proof, in that he never showed that the three cases he dealt with were the only three cases (Joyce 1).
     
    Euclid relied on the method of exhaustion in much the same way for proposition XII. 18, that spheres are to one another in triplicate ratio of their diameters, but instead of inscribing polygons to exhaust circles, polyhedra were inscribed to exhaust spheres. In Book XII of the Elements, Euclid demonstrates the rigor, the power, and the beauty of Eudoxus’ method of exhaustion. This method provided the ability to determine areas and volumes bounded by curves without the use of limits and is considered to be the predecessor of integral calculus (Aulie 1). Eudoxus, through his work in extending the theory of proportion and inventing the method of exhaustion, played a significant role in Euclid’s development of the Elements, considered to be one of the greatest works in history.

    Works Cited and Suggested Related Resources

    Aulie, Richard Paul. (Feb. 1, 2000). Eudoxus Of Cnidus, Method of exhaustion. Britannica.com. http://www.britannica.com/bcom/eb/article/6/0,5716,33776+3,00.html.

    Heath, Thomas L. The Thirteen Books of Euclid’s Elements, 3 vols., Dover (reprint), 1956.

    Joyce, D.E. (Feb. 2, 2000). Euclid’s Elements Book XII Proposition 2. (1996). Clark University. http://aleph0.clarku.edu/~djoyce/java/elements/bookXII/propXII2.html.

    Kline, Morris. Mathematical Thought from Ancient to Modern Times. New York: Oxford University Press, 1972.

    No author cited. (Feb. 2, 2000). Euclid of Alexandria. School of Mathematics and Statistics, University of St. Andrews, Scotland. (January 1999). http://www-history.mcs.st-andrews.ac.uk/history/Mathematicians/Euclid.html.

    No author cited. (Feb. 1, 2000). Euclid Elements toc,12 1. Perseus Project, Tufts University. http://www.perseus.tufts.edu/cgi-bin/text?lookup=euc.+toc,12&vers=english;heath.

    If you have any comments that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

    Return to my homepage.