
Department of Mathematics Education
J. Wilson, EMAT 6680

For more information about GSP, contact the publisher, Key Curriculum Press. To find instructions on setting up GSP as a helper application click here.
Discovery
Given any triangle ABC. Select a point P inside the triangle and draw lines AP, BP, and CP extended to their intersections with the opposite sides in points D, E, and F, respectively.
Explore (AF)(BD)(CE) and (FB)(DC)(EA) for various locations of P inside triangle ABC and for various types of triangles.
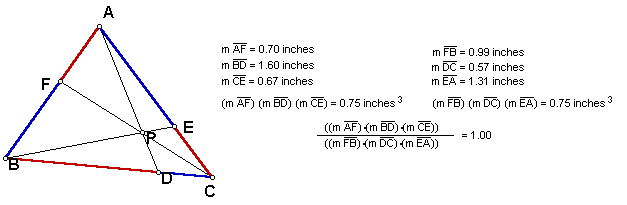
For all locations of P inside triangle ABC and for all types
of triangles, we come to the conjecture that
(AF)(BD)(CE) = (FB)(DC)(EA).
Click here to investigate for yourself.
Proof
In order to prove the conjecture, we want to use lines AD, BE, and CF, rather than the segments. We also want to construct parallel lines to try to find and use relationships within and between similar triangles.
Construct the lines AD, BE, and CF. Also construct parallel lines to line BE through points A and C.
Consider the triangles AFH and BFP.

Angles FHA and FPB are congruent because of alternate interior angles. In addition, angles HAF and PBF are congruent because of alternate interior angles. Therefore, triangle AFH is similar to triangle BFP by angle-angle similarity.
Therefore, by the fact that corresponding parts of similar
triangles are proportional we know the following:
AF/BF = AH/BP = FH/FP.
Consider triangles BPD and CID.
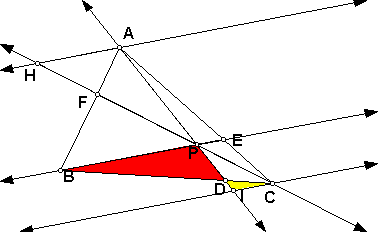
Angles BPD and CID are congruent because of alternate interior angles. In addition, angles PBD and ICD are congruent because of alternate interior angles. Therefore, triangle BPD is similar to triangle CID by angle-angle similarity.
Therefore, by the fact that corresponding parts of similar
triangles are proportional we know the following:
BD/CD = BP/CI = DP/DI.
Consider triangles CEP and CAH.
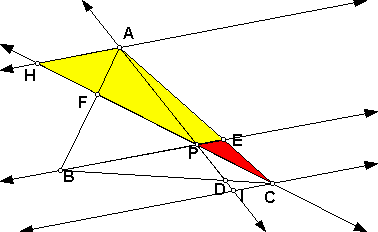
Angles AHC and EPC are congruent because of corresponding angles. In addition, angles HAC and PEC are congruent because of corresponding angles. Therefore, triangle CEP is similar to triangle CAH by angle-angle similarity.
Therefore, by the fact that corresponding parts of similar
triangles are proportional we know the following:
CE/AC = EP/AH = CP/HP.
Consider the triangles APE and AIC.
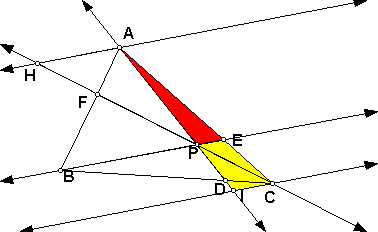
Angles AIC and APE are congruent because of corresponding angles. In addition, angles ACI and AEP are congruent because of corresponding angles. Therefore, triangle APE is similar to triangle AIC by angle-angle similarity.
Therefore, by the fact that corresponding parts of similar
triangles are proportional we know the following:
AE/AC = EP/CI = AP/AI.
Consider CE/AC = EP/AH and AE/AC = EP/CI. Through cross-multiplication we get (CE)(AH) = (AC)(EP) and (AE)(IC) = (AC)(EP). Therefore, substitution provides the relationship (CE)(AH) = (AE)(IC), so CE/AE = CI/AH.
Consider AF/BF = AH/BP, BD/CD = BP/CI, and CE/AE = CI/AH.
(AF/BF)(BD/CD)(CE/AE) = (AH/BP)(BP/CI)(CI/AH), so (AF/BF)(BD/CD)(CE/AE) = (AH/AH)(BP/BP)(CI/CI).
(AF/BF)(BD/CD)(CE/AE) = 1, therefore,
(AF)(BD)(CE) = (FB)(DC)(EA) for any point P located inside any triangle ABC.
Extension 1
The result of (AF)(BD)(CE) = (FB)(DC)(EA), can be generalized so that point P can be outside of any triangle ABC. If you investigated the original sketch, you noticed that when you tried to move point P outside of triangle ABC was "lost". In order to investigate when point P is outside of triangle ABC, the key to the construction is to use lines when constructing triangle ABC, instead of segments. Click here to investigate for point P outside of triangle ABC.
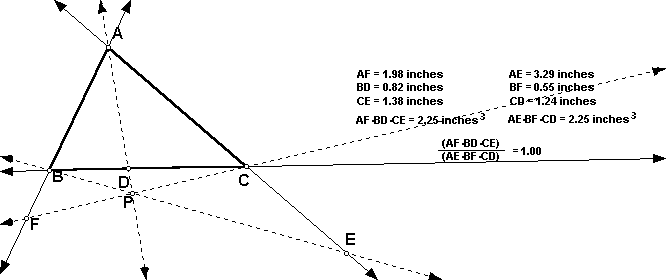
Therefore, we can generalize the original statement to
(AF)(BD)(CE) = (FB)(DC)(EA) for point P, inside
or outside of any triangle ABC.
In fact, the only restriction on the location of point P is that
P can not be a vertex of triangle ABC.
Extension 2
When point P is inside any triangle ABC the ratio of the areas of triangle ABC to triangle DEF is always greater than or equal to 4. Click here to investigate.
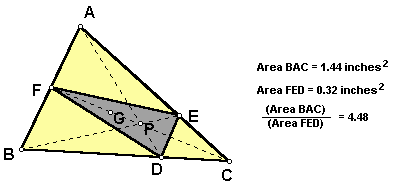
The ratio of triangle ABC to triangle DEF is equal to 4 when point P is the centriod of triangle ABC.
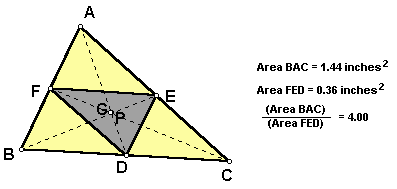
When point P is the centroid of triangle ABC, segments AD, BE, and CF are medians of triangle ABC. Therefore, points D, E, and F are the midpoints of segments BC, AC, and AB, respectively. Triangle DEF is the medial triangle of triangle ABC. Therefore, triangle ABC has 4 times the area of triangle DEF. (Note: The previous statement is true because triangle ABC is similar to triangle AFE in a ratio of 2:1, using the triangle midsegment theorem and properties of parallel lines. In addition, triangle AFE is congruent to triangle DEF, using properties of parallel lines. Therefore, the ratio of areas of triangle ABC to triangle DEF is 4:1.) Consider the relationship (AF)(BD)(CE) = (FB)(DC)(EA). When point P is the centroid, (AF)(BD)(CE) = (FB)(DC)(EA) = (ED)(EF)(FD). When point P is any other point inside triangle ABC, (AF)(BD)(CE) = (FB)(DC)(EA) > (ED)(EF)(FD). Therefore, the ratio of the areas of triangle ABC to triangle DEF is greater than 4:1.
If you have any comments concerning this investigation that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return to my homepage.