Note: I recommend that this page be printed out, so that the instructions are easier to follow.

In order to successfully complete a proof, it is important to think of the definition and the construction of a rhombus.
In the following outline, I will provide the statements, you provide the reasons.

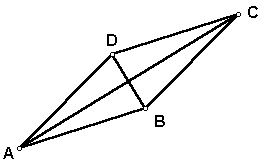
Prove: If a quadrilateral is a rhombus, then the diagonals are perpendicular bisectors of each other.

Given: Rhombus ABCD with diagonals BD and AC intersecting at point M.

Prove: Segment AC and BD are perpendicular bisectors of each other.

• A rhombus is a parallelogram, so the definition and properties of a parallelogram apply to a rhombus.
• Consider how a rhombus is constructed------parallel lines.
• Consider properties of parallel lines and vertical angles.
• The diagonals create 4 triangles.
• Consider triangle congruency properties.
• Click here to investigate this sketch to help with the steps of the proof.

Proof:

First we will prove that the diagonals are bisectors of each other.

1. Angle DBA is congruent to angle BDC.
2. Angle CMD is congruent to angle AMB.
3. Triangle CMD is congruent to triangle AMB.
4. Segment AM is congruent to segment MC.
5. M is the midpoint of segment AC.
6. Segment BD bisects segment AC.
7. Segment BM is congruent to segment MD.
8. M is the midpoint of segment BD.
9. Segment AC bisects segment BD.

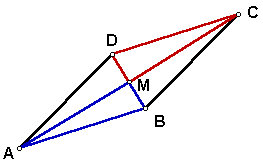
Then we will prove that the diagonals are perpendicular to each other.

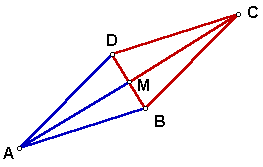
10. Segment CD is congruent to segment CB.
11. Segment BM is congruent to segment MB.
12. Segment CM is congruent to segment CM.
13. Triangle CDM is congruent to triangle CBM.
14. Angle CMD is congruent to triangle BMC.
15. Angle CMD + angle BMC = 180
16. Angle CMD = 90 and angle BMC = 90
17. Angle AMB = 90
18. Angle CMD is congruent to angle DMA.
19. Angle DMA = 90
20. Segment AC is perpendicular to segment BD.

Extension:

1. We could have made this proof much shorter, if we had used a particular property. Do you know what property we could have used to reduce the first 9 steps of proving that the diagonals are bisectors of each other down to one step? If so, state the property.
2. Transform the two-column proof into a paragraph proof.
3. Find an alternative way to prove that the diagonals of a parallelogram bisect each other.

If you have any questions while trying to complete this investigation, or suggestions that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.

Return to the Table of Contents.