

Dr. Wilson provides this challenging problem as an example to demonstrate the power of Geometer's Sketchpad (GSP) in exploring, discovering, and developing a construction. In addition, Dr. Wilson raises the point that many extension problems can be investigated using the completed construction. To read his full investigation and other related problems, link to EMAT 6680 Assignment 7 .
The use of GSP provides the ability to expand the number of topics, and increase the depth of study within each topic, that can be realistically covered successfully in today's high school geometry cirriculum. A difficult challenge for teachers is to determine an appropriate balance between these two factors in creating a course that is as rich as possible for students, while meeting/exceeding established cirriculum standards. Investigating tangent circles provides and excellent example of how a teacher can, and should be, creative in designing investigations that achieve this balance.
For more information on GSP, contact the publisher, Key Curriculum Press. To find instructions on setting up GSP as a helper application click here.
The following investigation is an example of one way that I feel that Dr. Wilson's assignment could be adapted for use within a high school classroom.
1. Use Dr. Wilson's assignment 7, to complete the construction of tangent circles described above and make a script. Your script should produce a sketch that appears similar to the following sketch, where circle O and circle M are the given circles. If you are having a great deal of difficulty completing this construction, click here for a script that can be used as a reference in creating your own script.
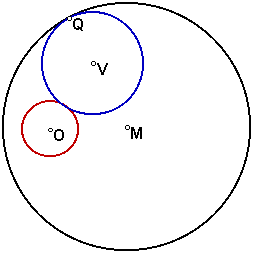
2. Notice that the tangent circle V that you have constructed is internal to circle M, but external to circle O. It is also possible to construct a tangent circle, so that circle O is internal to the constructed circle V. This construction is quite similar to your first construction. Your construction steps are the same to the point pictured below.
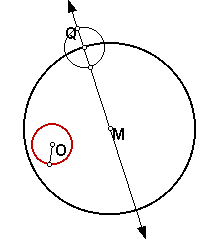
Now, construct segment and line TO.
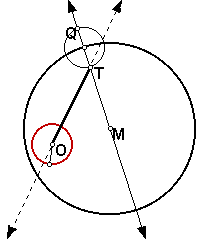
Construct the midpoint and perpendicular bisector of TO. The point of intersection S will be the center of the tangent circle.
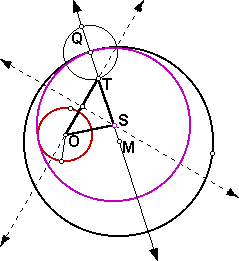
Make a script for this construction and be sure to hide all construction lines so that just the three circles are visible when the script is played. Your script should produce a sketch similar to the one below. If you are having a great deal of difficulty completing this construction, click here for a script that can be used as a reference in creating your own script.
3. Now we are going to take a look at the loci of the centers of these two tangent circles, circles V and S in the preceeding diagrams. In all of the sketches provided, circles O (red) and M (black) are the given circles, and circles V (blue) and S(purple) are the tangent circles. There are many cases to consider. Just click on the case and double-click animation in the sketch. In each case, describe the shape of the locus of each center and explain why this shape is produced.
4. Discuss for each case how you could show that each locus is the shape that you believe it to be. Think of the definintion of various conic sections. The hint I provided for you for case 1 provides a good start.
5. There are more cases that can be investigated. For example:
If you have any comments concerning this investigation that would be useful, especially for use at the high school level, please send e-mail to esiwdivad@yahoo.com.
Return to my homepage.