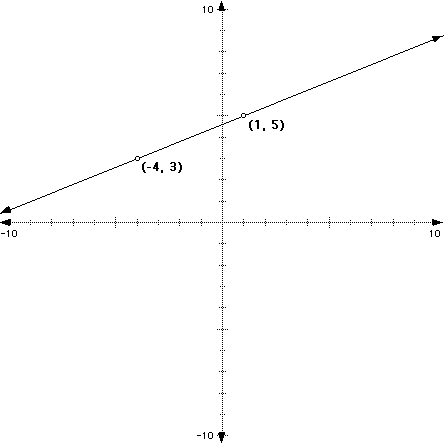
We get the following illustration when we plot the points (-4, 3) and (1, 5) and draw the between them:

Notice right away that this is a positive slope.

Next, because the defintion of slope is "the change in y-values over the change is x-values" or,

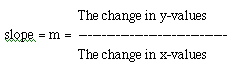
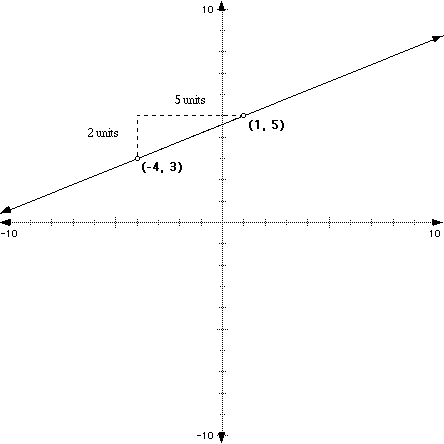
we can count up "rise vertcially" from the point (-4, 3) until we are abeam the point (1, 5) and then "run horizontally" over to the point (1, 5) to get our values for rise and run.

Look at the picture below. See, we "rise" 2 and then "run" 5 to get from one point to the next.

What about if we wanted to go from the point (1, 5) to (-4, 3) by moving left first then down? Well, it shouldn't make a difference how you move because the points are on the same line, but let's see:

If we started with the point (1, 5), we would move down vertically, which would give us a negative 2 movement. Then we would move right across to the point (-4, 3) which would give us a negative 5 movement as the illustration shows below.

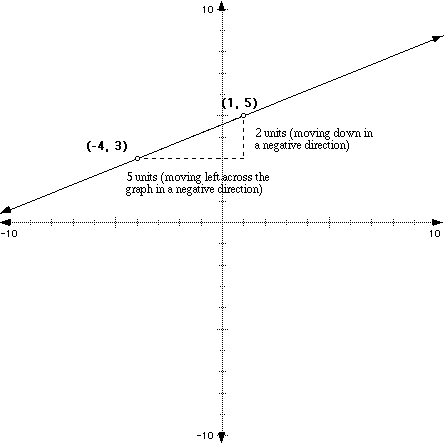
So if we move down 2 and then across negative 5, our change in y over the change in x would be -5/-2 which is 5/2. So, as long as you perform all of the movements and calculations correctly, it won't matter where you start and stop (which points you pick) on the graph when discovering the slope of the line between two points.

Now, algebraically, let's substitute the corresponding values of the coordinates into our slope formula:

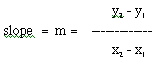
So,

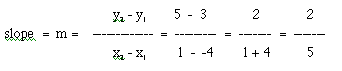
which is the same as we got graphically!