
By T. Barron & S. Kastberg

The quadratic formula is used to solve for x in a quadratic function. It can be derived from using the general form of the quadratic equation, y = a x2 + bx + c, by setting the equation = 0 and using the "completing the square" technique that we used in the previous less to solve for x.
If we perform these calculations, we end up with a formula that solves any quadratic equation for x.
The quadratic formula is:
where "a" is the coefficient of the x2 term, "b" is the coefficient of the x term, and c is the constant.
So, why do we need to know the quadratic formula? Well, in a previous lesson, when we were trying to find the x-intercepts, we could only approximate them because we didn't know how to solve the equation, y = -3x2+ x + 1. We said the the x-intercepts were approximately x = -0.8 and x = 0.4. , but we couldn't tell for sure.
So, let's use quadratic formula to solve for the x-intercepts.
To find the x-intercepts of any equation, substitute 0 in for y and solve for x.
So, we have 0 = 3x2+ x + 1. Now, use the quadratic equation to solve for x, wich a = 3, b = 1, and c = 1:
So, now we can find the value of the x-intercepts and not have to estimate!
What about if there are no x-intercepts?
Consider the quadratic function: f(x) = x2 - 3x + 5.
Here, a = 1, b = -3 and c = 5
Let's find the y-intercept first:
To find the y-intercept, substitute 0 in for x and solve for f(x):
So the y-intercept is (0, 5).
Now, let's find the vertex:
To find the x-value of the vertex, use the formula x = -b/2a.
So,
To find the y-value of the vertex, substitute 3/2 in for x
in the equation ![]() , and solve for
f(x):
, and solve for
f(x):
So, the vertex is (3/2, 11/4)
Finally, let's find the x-intercepts by using the quadratic formula.
To do this, we set the y-value (or f(x)) = 0 and solve for
x. So, take the function ![]() , and set it equal
to 0:
, and set it equal
to 0:
![]()
Now use the quadratic formula where a = 1, b = -3, c = 5
![]()
![]()
![]()
![]()
Well,![]() is not a real number. If you try
to "plug"
is not a real number. If you try
to "plug" ![]() into your calculator,
you will get an error. So, if we can't solve for x, that means
there are no x-intercepts. Let's graph the parabola using the
y-intercept (0, 5) and the vertex (3/2, 11/4). Remember, the parabola
should not cross the x-axis anywhere. Also, remember since "a"
is positive, the graph should open upward. Let's see!
into your calculator,
you will get an error. So, if we can't solve for x, that means
there are no x-intercepts. Let's graph the parabola using the
y-intercept (0, 5) and the vertex (3/2, 11/4). Remember, the parabola
should not cross the x-axis anywhere. Also, remember since "a"
is positive, the graph should open upward. Let's see!
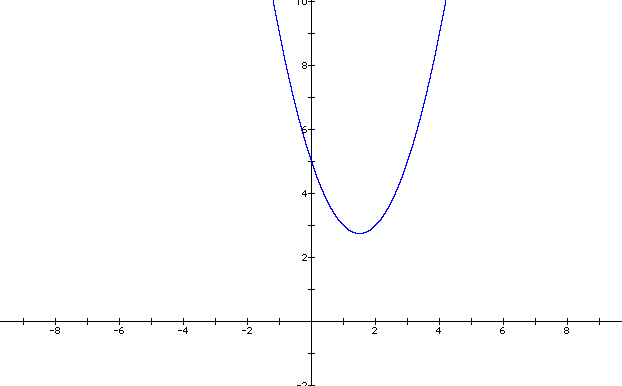
So, as we can see, being able to use the quadratic formula is quite important when graphing quadratic functions!
Graph the quadratic functions below by finding the y-intercept, the x-intercept(s) and the vertex of each function.
1. f(x) = - x2 - 4x + 1
2. f(x) = 2 (x + 1)2 - 7
3. f(x) = -5x2 + 2x - 1
4. f(x) = x2 - x
5. f(x) = (x - 3)2