Click
to check the practice problems from Right Triangles, Altitiudes,
and the Geometric Mean.
Review:
We have the following theorems so far:
Similarity Theorem: The altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse creates two triangles, both of which are similar to the original triangle and each other.
Right Triangle Altitude Theorem :
Part a: The measure of the altitude drawn from the vertex of the right angle of a right triangle to its hypotenuse is the geometric mean between the measures of the two segments of the hypotenuse.
Part b: If the altitude is drawn to the hypotenuse of a right triangle, each leg of the right triangle is the geometric mean of the hypotenuse and the segment of the hypotenuse adjacent to the leg.
Recall our right triangle with an altitude drawn from the hypotenuse of the right triangle:
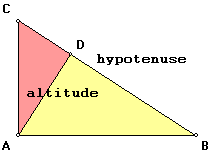
From the theorems following facts follow:
ABC is similar to 
DAC
ABC is similar to 
DBA
and
DAC is similar to DBAAnd that the measures
- 1.
- 2.
- 3.
In your Journal, sketch the triangle above and all the facts below it. Write the associated theorem next to each fact.
Now let's just look at and. Write these down in your notebook and square
both sides of each equation.
We get 
and 
.
In your notebook create a new equation by adding the two equations. Leave the two squared terms on the left, the others on the right side of the equation.
Factor a common factor on the right side. Look at the triangle again:
What is the sum the sum of the right hand side? Substitute this in. What do you have?
Check
your work and correct your notebook if you made any mistakes.
Using the words hypotenuse and legs of a right triangle, how would express your results in word?
Pythagorean Theorem:
In a right triangle, the sum of the squares
of the measure of the legs equals the square
of the measure of the hypotenuse.
In the picture the above theorem states: 
Activity 1: Draw the following in your Journal. Write the questions and answers.
Notice the four triangles all congruent.
What is the area of the biggest square created by the triangles? ___________
What is the area of each triangle? ___________
What is the area of the smaller square?_____________
Click the check and make sure your work is correct.
We now know the area of the inside square. What is the length of the side ? It is the square root. Notice the sides of the square are the hypontenuse of each of the congruent triangles.
The following list is a link to GSP proofs/demostrations of thePythagorean Theorem. Check them out. Choose one and write in your Journal how it proves or demonstrates the Pythagorean Theorem. Make prints of the sketches as you neeed.
Click
the lightbulb to practice this lesson