isosceles triangle
 In an isosceles triangle, two of the
three sides of the triangle have the same length.
The triangle to the right
is an isosceles triangle, even though it may be hard to tell.
Scroll down for sure-fire
ways to tell if a triangle is isosceles or not.
In an isosceles triangle, two of the
three sides of the triangle have the same length.
The triangle to the right
is an isosceles triangle, even though it may be hard to tell.
Scroll down for sure-fire
ways to tell if a triangle is isosceles or not.
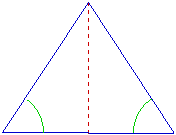 In the
above triangle, the red dashed line is called an altitude. It is the perpendicualr
line from the midpoint of the base to the opposite vertex. It forms two
right triangles.
If we can
show that these two right trianglesare congruent, then we can prove that
the above triangle is indeed an isosceles triangle.
We know
that the altitude bisects the base so now we have two sides of the two right
triangles are congruent. Since the right angles are in between these two
sides we can see that by side-angle-side, we have two congruent triangles.
Thus the two hypotneuses are congruent so we indeed have an isosceles triangle.
Notice
that the two base angles are also congruent. This is a property of isosceles
triangles.
In the
above triangle, the red dashed line is called an altitude. It is the perpendicualr
line from the midpoint of the base to the opposite vertex. It forms two
right triangles.
If we can
show that these two right trianglesare congruent, then we can prove that
the above triangle is indeed an isosceles triangle.
We know
that the altitude bisects the base so now we have two sides of the two right
triangles are congruent. Since the right angles are in between these two
sides we can see that by side-angle-side, we have two congruent triangles.
Thus the two hypotneuses are congruent so we indeed have an isosceles triangle.
Notice
that the two base angles are also congruent. This is a property of isosceles
triangles.
Click
here for a GSP script to form an isoscoles triangle given an altitude,
then a base.


