Similar triangles are defined as two triangles, ABC and DEF, that hold the following property:

Now I will use the measurement and calculator features of GSP to see if these two triangles are similar.

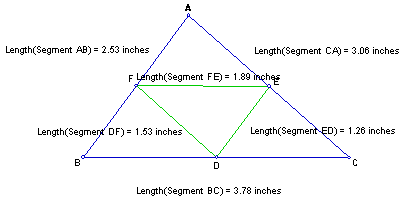
Using the calculator on GSP we see that:

Length(Segment AB)/Length(Segment ED) = 2.00
Length(Segment BC)/Length(Segment FE) = 2.00
Length(Segment CA)/Length(Segment DF) = 2.00

BUT, we must also verify that these two possibly similar triangles have congruent corresponding angles. Once again I will use the measure tool of GSP to explore this.

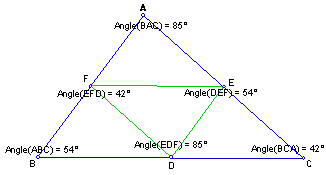
Angle(ABC) = 54° Angle(BCA) = 42° Angle(BAC) = 85°
Angle(DEF) = 54° Angle(EFD) = 42° Angle(EDF) = 85°

Thus we can see that the corresponding angles are congruent and the two triangles are congruent.

back