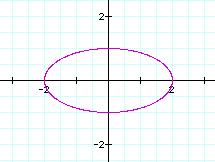
Consider the graphs generated from the following parametric equations the graphs of which appear below. Can you guess which equation generates a circle of radius one and which one generates a circle of radius two?

Since the values for x and y are based on the angular value t, x = a cos (t) and y = b sin (t), if a = b we have simplifying and using trigonmetric identities we have . Hence if a = b we have a circle with radius a.

If a > b in the parametric equations , then an ellipse centered at the origin with a major axis of length 2a units and a minor axis of length 2b units is generated. An example follows.

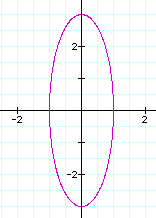
If a < b in the parametric equations , then an ellipse centered at the origin with a major axis of length 2b units and a minor axis of length 2a units is generated. An example follows.

Although, at first glance, the graph of the parametric equation

may look like a line it is not! It is actually a degenerate ellipse. Cosider the case where a=b and h = 2

Consider the following system of parametric equation where a = b and h = 2:

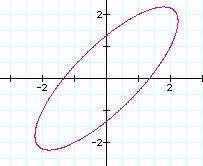
Note that the major axis is on the line y=x. This will be the case regardless of the relationship between a and b as the following example will illustrate.

Note that the major axis in this example is still the line y = x.

Can you guess why the major axis in the same in both of these example? Perhaps one more example will help.

Note in this example the h values are not the same, hence the major axis is not y = x. In addition the orientation will change if the h value is less than zero as the example below will illustrate.

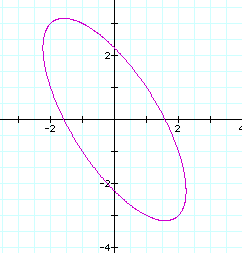
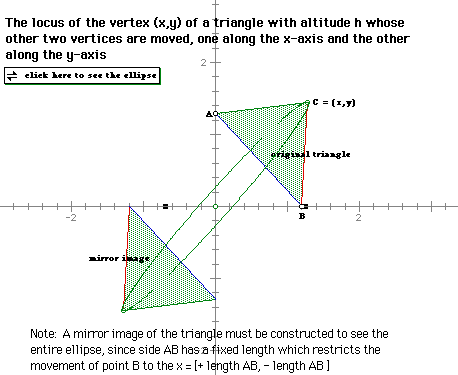
The parametric equations of the form describe the locus of the vertex (x, y) of a triangle with altitude h whose other two vertices are moved, on along the x-axis and the other along the y-axis. To see the ellipse generated using GSP click HERE or create one yourself using the following sample.

Return