

Problem 1: Construct a triangle and its medians. Construct a second triangle with the three sides having the lengths of the three medians from your first triangle. Find some relationship between the two triangles. (E.G. are they congruent? similar? have same area? same perimeter? ratio of areas? ratio or perimeters?) Prove whatever you find.
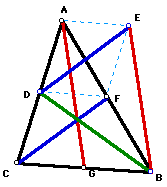
Triangle ABC is the given triangle. Segments CF, BD, and AG are the medians of that triangle. Triangle BDE is the new triangle constructed with the medians of the first triangle. The dashed lines are simply put in to help us with some proofs later on.
If you would like to investigate the above construction, make sure GSP is open and then click here.
After some investigations, we discovered that there is basically no relationships between the two triangles regarding the ratio of perimeters or angles. They are not congruent triangles or even similar ones.
The only relationship that we discovered was that the area of triangle BDE is 3/4 the area of triangle ABC. Now all we have left to do is to prove the above theorem.
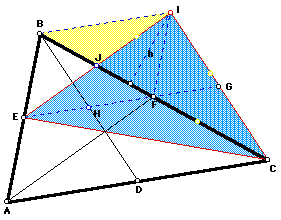
We want to show that the area of triangle EIC is 3/4 the area of triangle ABC. BIDC is a parallelogram, therefore triangle BIC and triangle BCD have congruent areas.
Because EJ is parallel to AF and EJ bisects AB then EJ also bisects BF. As a result BJ = JF and therefore JC =3/4 (BC). We will now substitute 3/4 (BC) for JC. We now have the following equations.
The area of triangle ABC is twice the area of triangle BDC because of the definition of medians. (Remember that the area of triangle BDC is = the area of triangle BIC.)
The area of triangle EIC is twice the area of triangle IJC.
After cancelling out the fractions we are left with the fact that:
If those 2 formulas are placed in a ratio the [BC * h] cancells out leaving us with the ratio of areas of triangle EIC and ABC to be three-fourths. (End of proof)
After further investigations we discovered that there is somewhat of a relationship regarding the ratio of the perimeters of the 2 triangles. The ratio is always in a range from .7 to .9. We have no explanation as to why this is, but we still chose to point out that we noticed this relationship.