---

Problem:

15. Find the triangle of minimal perimeter that can be inscribed in a given triangle. (For a start, you may want to restrict your investigation to
the given triangle being acute.)

To investigate this on your own: Click Here.

To investigate starting with an equilateral triangle: Click Here.

(You must have GSP on your computer in order to do this.)

For those without GSP (Geometre's Sketch Pad - computer software), we start by constructing a triangle.

Next, we construct points on each of the sides of the triangle.

The idea is to move points D, E, and F such that the triangle DEF will have a minimum perimeter.

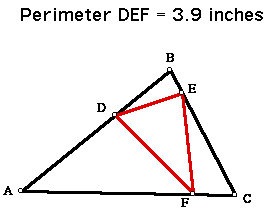
Of course,one obvious set of points that we would like to try would be the midpoints of the sides of triangle ABC.

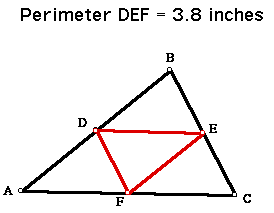
Let's try the points near the endpoints of the shortest side (BC in this case).

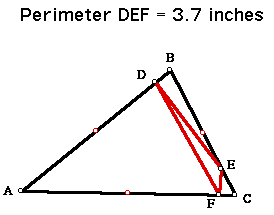
Does any of this change if the original triangle is an obtuse triangle?

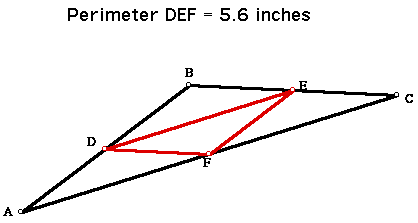
This is with the inscribed triangle at the midpoints. Now see what happeends when the vertices of triangle DEF are near points B and C.

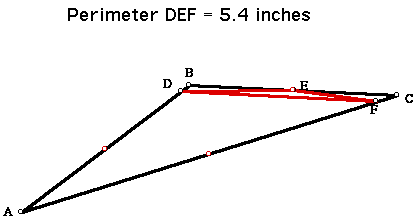
Let's try an equilateral triangle:

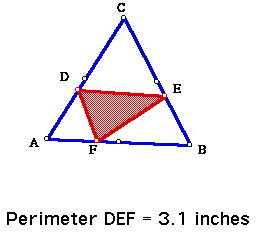
Now put points D, E, and F at the midpoints of the sides of triangle ABC.

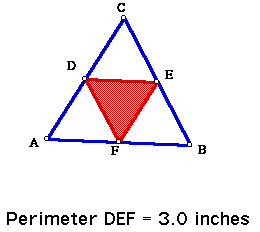
Let's try points D, E, and F near any one of the vertices of triangle ABC:

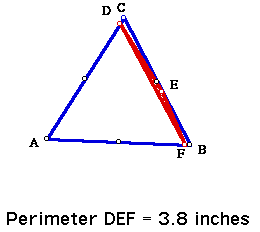
Any ideas or conjectures? Keep on trying. I can't give away all of the answers.

Return to Chris McCord's EMAT 6680/Home Page

Return to Chris McCord's EMAT 6680 Assignment Index Page