Write- up # 4

for

Jenni McIntire

Problem 7 in assignment 4

First construct the orthic triangle of an acute triangle. The orthic triangle connects the feet of the altitudes.

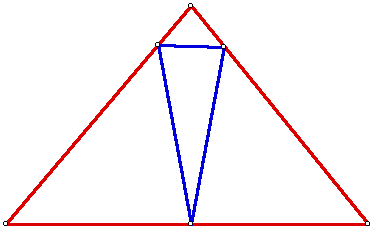
We then construct G, H, C, and I for the original triangle (G1, H1, C1, and I1) and the orthic triangle. We notice that there are 8 labels but only 7 points. Which one is missing? If we look at the colors, we see that we a missing one of the orthocenters. It turns out that the orthocenter of the original is the same as the incenter of the orthic.

 

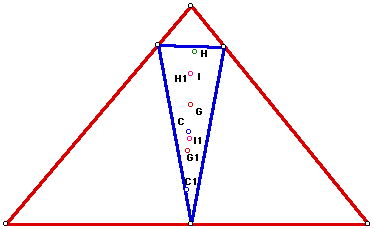
We ask the question, is this only true on an acute triangle. Lets find out.

Lets look at a right triangle.

 

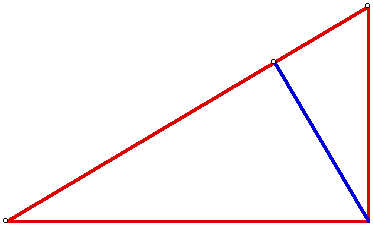
Since the legs of the right triangle are also the altitudes, the orthic triangle does not exist on a right triangle.

Lets look at an obtuse triangle.

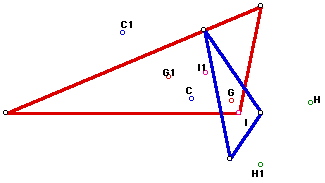
We now notice that we have both of the orthocenters, but the inenter of the orthic triangle is now the same as the vertex of the obtuse triangle.

Return