This page will investigate three polar equations:
![]() ,
,
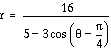 , and
, and
![]() .
.
Here is ![]() :
:
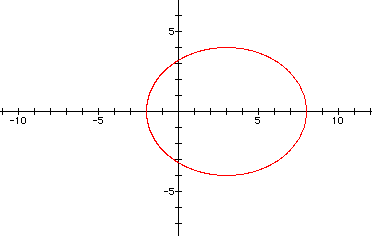
The graph is an ellipse, 10 wide and 8 tall, with a center (intersection of the segments joining foci) at (3,0).
What if we changed cosine to sine so that we have ![]() ?
Let's see:
?
Let's see:
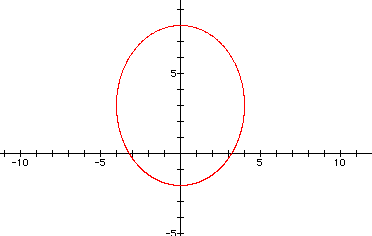
So by changing cosine to sine, the graph is now 10 all and 8 wide, with its center at (0,3).
Are these two graphs relflections af each other about an axis? a line? Putting both on one graph at a time helps:
Now what do you think about a reflection? What about a rotation? When may a reflection and a rotation give the same result?
Consider the line y=x in the graph:
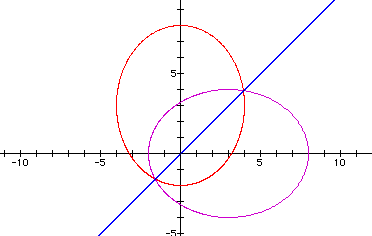
This line helps us see that the two ellipses are, in effect,
reflections of each other. The purple graph is rotated ![]() radians
to get to the red graph.
radians
to get to the red graph.
How does changing sine to cosine in the function effect this change? Email your hypothesis to me.
Now look at 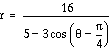 : Note that the
difference between this polar equation and the previous polar
equation is that we subtract a particular radian measure from
theta.
: Note that the
difference between this polar equation and the previous polar
equation is that we subtract a particular radian measure from
theta.
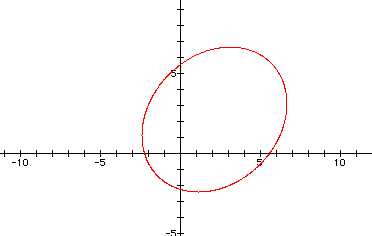
Compare this ellipse 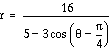 to
the previous polar equation
to
the previous polar equation ![]() by putting both on the same graph:
by putting both on the same graph:
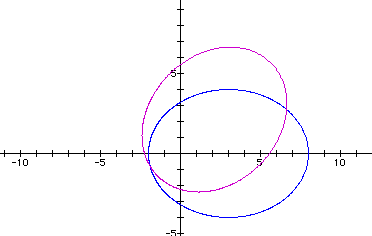
What rotation is effected? Use your hypothesis to predict what
the graph of 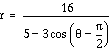 (red) looks like. How will it compare
to the graph of
(red) looks like. How will it compare
to the graph of ![]() (green)? Let's put
them both on the same graph:
(green)? Let's put
them both on the same graph:
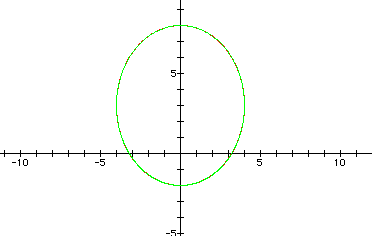
They are the same. Explain why this is true. Email your conclusion to me.
What do you think you can predict about the graph of ![]() ?
?
What might cause asymptotes? Can you predict the location of any asymptotes? Look at the graph now:
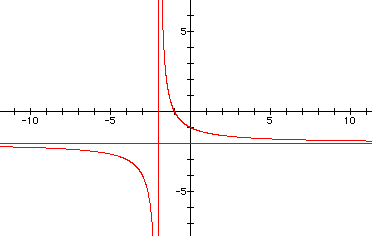
In the above, the curved lines give the graph while the straight lines are asymptotes.
Use your calculator to determine r when theta = .99 pi, .99999 pi, then try 1.99 pi and 1.99999 pi. Finally, try theta = pi and 2 pi. Explain your answers in an email to me.
RETURN TO HOME PAGE