
Tangent Circles
by Jamila K. Eagles
This exploration begins with the problem: Given two circles and a point
on one of the circles, construct a circle tangent to the two circles circles
with one point of tangency being the designated point.
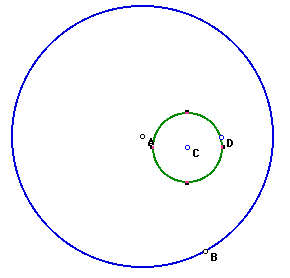
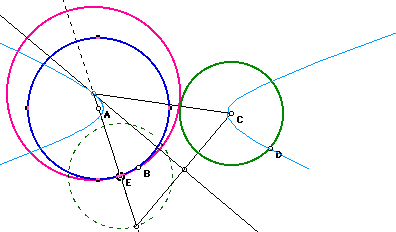
In this case, our arbitrary point is E and the construction looks like
the picture below. We know that the segment connecting the centers of the
two given circles is always the length of the sum of the radius of the desired
circle plus the radius of the given circle that did not have the specified
point. The same distance can be laid off along the line through the given
point from the center of the desired circle through a point on a constructed
circle with center at the given point , and radius of the given circle that
did not contain the specified point. Now connecting center point of circle
C and the center point of circle E, we have an isosceles triangle. The center
of our desired circle lies on the perpendicular bisector of the base of
our isosceles triangle. Using GSP, we can construct a circle with center
at the point where the perpendicular bisector of the base of our triangle
and the line that goes through the given circle with the specified point
intersect. The radius of our desired tangent circle is equal to the segment
formed between the intersection and point E( since the circle must go through
point E).
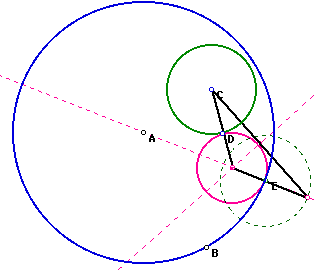
Now we want to consider the locus of the center of our circle tangent
to two given circles. Using GSP, we can trace the center point of the new
circle as the given point E travels around our given circle A (dark blue).
Tracing this point giveus us an ellipse with foci at the centers of the
given circles(light blue).
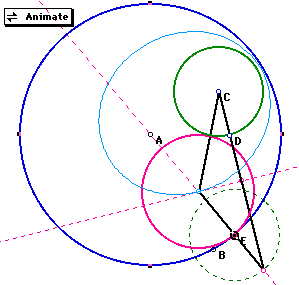
Now we want to look at other cases. We will take a look at what happens
when the given circles are two intersecting circles. Using GSP to trace
the center of our tangent circle(pink), We find that the locus of our center
point is again an ellipse with foci at the centers of the given circles
(light blue).
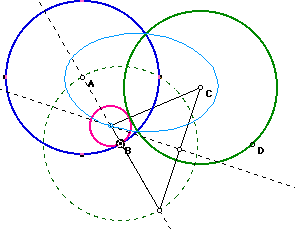
Our final case is the case where we have disjoint circles. The tangent
circle constructed is formed in pink in the picture below. By tracing the
center of our tangent circle once again, we see that this time the locus
of the point forms a hyperbola, but just like the previous cases, the foci
are at the centers of the given circles.
If given two circles and a given point on one of the circles, a new
circle tangent to both circles through the given point can be constructed.
Using geomerter's sketchpad, many concepts can be explored. In my exploration,
I found that depending on the case, the locus of the center point of a circle
tangent to two given circles can be an ellipse or a hyperbola, both having
loci at the center points of the given circles.






