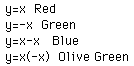
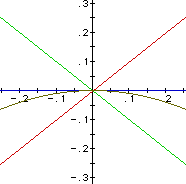
First, I began with very simple linear equations and I chose f(x)=x and g(x)=-x.i. h(x)=f(x)+g(x)
ii. h(x)=f(x)*g(x)
iii. h(x)=f(x)/g(x)
iv. h(x)=f(g(x))
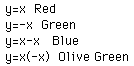

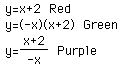
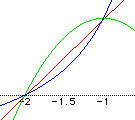
In this graph, the graphs of f(x), f(x)*g(x), and f(x)/g(x) intersect
at the points (-2,0) and (-1,1).
What happens when f(x)=x+2 and g(x)=x-3?
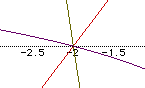
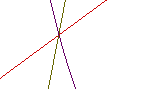
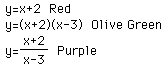
In the third investigation, there are still at least 3 graphs that intersect.
In this case, they are f(x), f(x)*g(x), and (f(x)/g(x). This matches up
with the graphs that intesected in the second set of linear equations.
Let's dig deeper into the problem. What would happen if f(x) and g(x) are
even more complex?
Let's let f(x)=5x-3 and g(x)=2x-5.
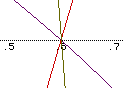
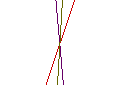
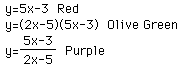
Once again the same three graphs of f(x), f(x)*g(x), and (f(x)/g(x) appear
and intersect.
So from this investigation, it SEEMS that for arbitrary linear equations,
f(x) and g(x), the graphs of f(x), f(x)g(x), and f(x)/g(x).
Though this is not even close to a proof, it is interesting to see that
there is something that causes these three graphs to intersect regardless
of the choice of linear equations.