Volume of a Box
Problem #2
Problem:
Given a rectangular sheet of cardboard 15 in. by 25 in. If a small square
of the same size is cut from each corner and each side folded up along the
cuts to form a lidless box.
What is the maximum volume of the box?
What size(s) of the square would produce a box of volume equal to 400 cubic
in.?
Below is a drawing (using GSP) of the cardboard before the actual cuts are
made:

The length of the box will be 25-2x. The width of the box will be 15-2x
and the height will be x. So the formula for the volume of the box will
be:
V = x (25 - 2x) (15 - 2x)
So using Microsoft Excel, we can find the maximum volume of the lidless
box. We need to remember that there are some conditions that apply:
25-2x>0 and 15-2x>0
Let's guess that we can find a value to begin searching for the maximum
volume by filling in a spreadsheet as follows:
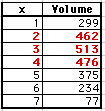
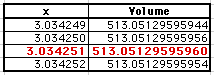
The values in red indicate where the volume peaks. From the spreadsheet
we see that the maximum value is 3, but the maximum value for the volume
may not be at an integer. So let's check some decimal values between 2
and 4:
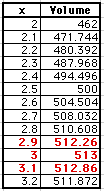
Again we see that the maximum value is at x=3. Now we need to decide
how accurate we want to be. This all depends on the situation. If this
box was being constructed in a factory in real life, how close we get to
the actual value depends on the accuracy and precision of the machine constructing
the box. I am going to assume for our purposes that we need to go a little
further to find a closer value; however, I am only going to display parts
of the spreadsheet used to figure this out (to conserve space).
Our next step is to try to find accuracy to a few more decimal places.
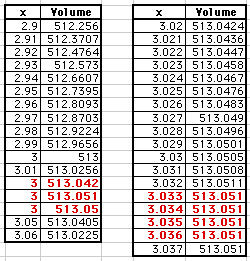
Notice in the second spreadsheet that there are several x-values that
produce the same volume. This problem will disappear with the next couple
of steps.
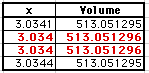
So, I think that 6 decimal places is enough for now. So the maximum
volume is achieved:
x = 3.034251
Maximum Volume = 513.05129595960 cubic in.
The rest of the question asked us to find when the volume=400 cubic
inches. The procedure is the same, if you want to find the volume the same
way we did above.
Setup your spreadsheet, and find value that are close to 400. The "zero-in"
on the actual values.
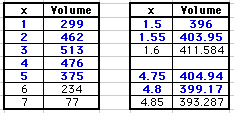
Notice that we have two values that produce a volume of 400 cubic in.
Again one needs to decide how many decimal places he or she needs. This
same procedure is continued until we find that:
x = 1.52935 and 4.792841
produce values very close to
400 cubic in.
Using the Solver command on the spreadsheet, it tells us that
x = 1.52492881302238
produces a volume of exactly
400 cubic in.
It is important to remind students that a computer is never 100% accurate.
Just like our hand-held calculators can only "remember" a certain
number of digits, a computer "remembers" more, but not an infinite
number of digits. Therefore, chances are that the volume is NOT exactly
400 cubic inches as the computer says. Also be aware that the Solver only
gives one value.
Return to Final Projects Page
Return to Write-Ups for EMT 668 Page
Return to Dawn's Home Page







