

This graph is still a flower, but the petals are different. With fractional
k values, our petals now overlap, which was not the case with integer values.
Instead of getting k number of petals, we get 2 times the numerator number
of petals.
Let's look at some of the other graphs with different k values.

This should remind you and your students of a design produced by a spirograph.

Again this is similar to the graphs a integer k values when a > b.
When the numerator is odd, the flower has the same number of petals as the
numerator. So this graph has 7 petals and does not meet at the origin, since
a > b.
When a < b, we again get 7 large petals. However, we also get 7 small
petals that overlap at the intersection of the other petals.

If we asked the students to guess how the graphs would change by using
k = j/3, they would probably say that the petals would overlap more than
they do when k = j/2.
Would they be correct? Let's see with 2 new graphs.
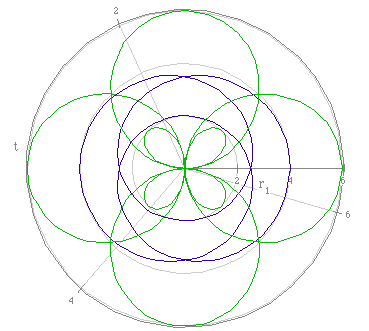
Yes, the students would be correct. The graph with a > b, acts like
the graphs of a > b and k as an integer value. The same is true for
the a < b. They only differences come from k being a multiple of 1/3.