Things To Think About
Linear Equation:
What happens at the ends of the graph? Obviously, we would not want to estimate
a time value that is less that 0. At time zero, the graphs are pretty far
apart. Then the line looks pretty good for the middle time values. But what
if we wanted to estimate the temperature after 40 minutes? By looking at
the graph, we can see that after the data point at time 30 minutes, we again
get deviation.
Since we know that all lines cross the y-axis (unless they are horizontal),
according to this graph the temperature of our water would be 0, eventually.
Does that make sense? That means that a glass of water sitting in a room
that is 70 degrees (F), will eventually freeze and the temperature will
continue decreasing to zero and below.
I don't think this is reasonable; therefore, we can rule out
a linear equation as being the one that we wanted.
Quadratic Equation
This investigation is very similar to the previous one.
Again what happens at the ends of the graph? In the quadratic graph, time
zero is not a problem. The quadratic graph dips lower than the graph of
the data. Also, at time 30 the graph differs radically.
If we remind the students that a parabola has its ends both going in the
same direction, this graph causes a problem, also.
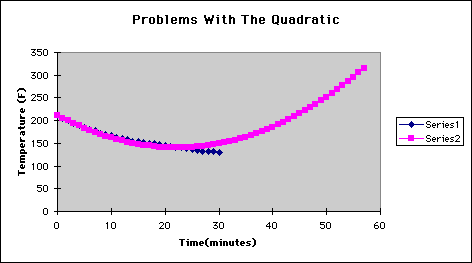
If a person looks at this graph without knowing what the data is, they
would conclude that the temperature of the water began to increase after
about 30 minutes. In fact, after 60 minutes the temperature is higher than
the we when we began.
Obviously, this is not a good way to represent the graph either.
Exponential Equation
This investigation is similar, but the results are different.
Look at what happens at the edge of the graph. There is not much difference
between the equation we formed and the data collected.
What properties does an exponential equation have that a linear and quadratic
equations do not have? Exponential equations are asymptotic. That is,
they "level off" at a certain point. Using this type of graph
eliminates our water freezing in room temperature as in the linear graph
and the water reheating itself in room temperature as in the quadratic graph.
So it seems that this type of equation is the best to try.
Return to the Combining Science
and Math Page
Return to Dawn's Home Page

