Centroid of a Triangle
The centroid of a triangle is the common intersections of the three medians.
Circumcenter of a Triangle
The circumcenter of a triangle is the point in the plane equidistant from
the three vertices of the triangle. The point equidistant from two points
lies on the perpendicular bisector of the segment determined by the two
points. The circumcenter lies at the intersection of the three lines.
Orthocenter of a Triangle
The orthocenter is the common intersection of the three lines containing
the altitudes. An altitude is a perpendicular segment from a vertex to the
line of the opposite side. The orthocenter of a triangle may be outside
of the boundaries of the triangle.

Circumcircle of a Triangle
The circumcircle of a triangle is the circumscribed circle. Its center is
the circumcenter.
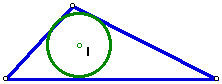
Incircle of a Triangle
The incircle of a triangle is the circled centered at the incenter. The
incircle is also tangent to all three sides of the triangle.

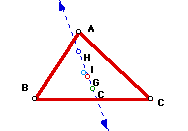
Centers of a Triangle
This script produces the 4 centers (circumcenter, orthocenter, centroid,
and the incenter) of a triangle.
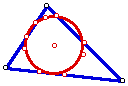
Euler Line
The line containing the circumcenter, the orthocenter and the centroid of
a particular triangle.
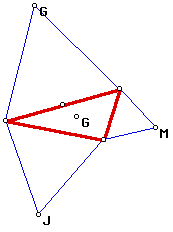
Nine Point Circle
The Nine Point Circle for a trianlge passes through the three midpoints
of the sides, the three feet of the altitudes, and the three midpoints of
the segments from the respective vertices to the orthocenter.
Given a triangle construct 3 equilateral triangles
on each side of the original triangle.
Click on the triangles above to see an animation of this construction.
Given a triangle construct a square on each
side of the original triangle.
Click on the triangles above to see an animation of this construction.