
Write Up #2
For demonstration, is it better to graph 5 graphs at once or produce them in sequence adding one at a time? What are the pedagogical implications of this observation?
Let us consider several possible classroom scenarios:
Scenario #1
Joachim Johnson, a teacher at Davis High School, shows his class the following picture, which he says he prepared just before class as the students were filing in:

After the oohs and aahs have secceeded, he asks the students how the parabolas appear to be related to one another. The only sounds in the room are Joachim's heartbeat and the concentrated chewing of Wrigley's. Over the next 20 minutes, Joachim points out the different parabolas, where their vertices are, and how they "match up" with their corresponding equations. Anita, who sits on the front row--not by choice--is heard to exclaim as she darts out of class, "Wow, those U-shaped graphs are going to be tough. I looked ahead in the book and we have to do this stuff for a whole chapter!"
Scenario #2
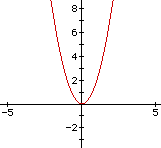
Juanita Wichita, a teacher at Rocky Mountain High School, shows her class the following graph:

"Remind me, and Anita, since she was at the Cross Country Meet--placing 2nd, I might add-- what we know about this from yesterday's class," she says, knowing the students were expecting just such a request. Nathan says it is a parabola and Quay says the vertex is at the origin.
"What about the equation that might have produced this graph?," Miss Wichita asks. Caroline says that it must have started with a positive number " 'cause its openin' up." Dan says, "I bet the equation is y equals x squared."
"Wow," says Miss Wichita, "I'm impressed with your memory. You'd think we talked about that all day yesterday." Dan leans forward and tells Annette, "She must have said the word vertex 50 times yesterday--how could we not remember what it is?"
"Well Dan, you are right, that is the equation of this parabola. Now, let's look at another:"
"Can you say anything different about this parabola?," she asks. Silence permeates and Dan finally says, "Well, we thought you were going to show us a different graph."
"Allright, I'll help you out. Here is a picture of both parabolas on the same coordinate system:"

"Oh, and by the way, here are the equations of these two parabolas:"
"Take 23 seconds and decide which equation belongs to the green parabola and which belongs to the red. Come up with a hypothesis for why they are different sizes."
Conversation continues as the students share their conjectures. They ask Miss Wichita to try their conjectures and decide as a class that multiplying by a constant tends to "stretch" the parabolas, or make them skinnier.
Next, Miss Wichita breaks the class into groups of three and the students are invited to discover other variations of the parabola--moving the parabola's vertex along the x-axis, along the y-axis, and out into the quadrants. Their final goal is to come up with a picture that looks as much like the following picture as possible:

Debriefing
For demonstration, in my opinion, it is better to produce graphs in sequence. This teaching strategy encourages creative thinking and individual/group discovery. Although at times impressive, starting with 5 graphs can be overwhelming to the students and tends toward a lecture. It is re-creative by nature as opposed to the creation that results from graphing in sequence.