Write-up 2

Assignment #2 Problem #10
A discussion of the equation:

by: Kelli Nipper

The graph of an equation in two variables (x and y), is the set of all points (x,y) that satisfy the equation.

To begin our investigation, we will consider when a = 0, 1, 2, and 3.

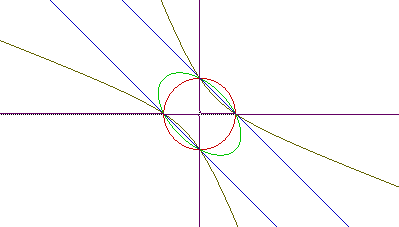
From this graph, four shapes are recognized.

1) When a = 0 (red), the distance formula tells us that the graph of x^2 + y^2 = 9 is a circle centered at the origin with a radius of 3. More generally, the graph of the equation is (x-h)^2 + (y-k)^2 = r^2 , with radius r and center (h,k). When h and k are not both 0 (at the origin), the circle is translated h units right or left and k units up or down.

2) When a = 1 (green) , the graph of x^2 + xy + y^2 = 9 is an ellipse. The conventional form for an ellipse would be:

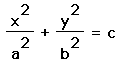
Since the ellipse is rotated 45 degrees from the axis, there is an xy term. Using the formulas for the rotation of axes:

x = x' cos 45 - y' sin 45
y = y' sin 45 + y' cos 45

we find that the equation for the same ellipse with its foci on the y-axis would be:

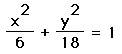
3) When a = 2 (blue) , the graph of x^2 + 2xy + y^2 = 9 is two parallel lines. This becomes obvious when you factor.

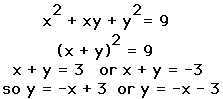
These are equations of 2 lines with y intercept at 3 or -3 and slope (m) at -1.

4) When a = 3 (tan), the graph of x^2 + 2xy + y^2 = 9 is a hyperbola. The standard form for a hyperbola is:

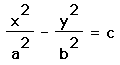
This introduces the same situation as with the ellipse, in that the rotation causes an xy term.

These four different shapes for the equation

make you wonder what happens inbetween the values a = 0, 1, 2 and 3.

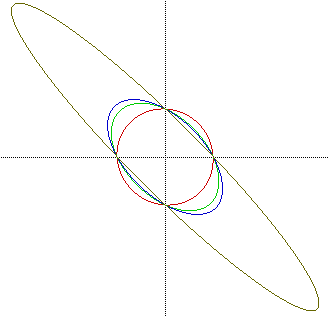
First, I investigated the transition between the circle (a = 0) and the straight lines (a = 2).

The following graph (a = 1/10, 9/10, 11/10, and 19/10) shows that when 0 < a < 2, the graph is an ellipse that approaches a circle when a is very small, and approaches two straight lines when a gets close to 2.

This indicates that 0 and 2 are boundaries.

The following graph shows that as a gets large (above 2), the hyperbolas sharpen and narrow approaching the axes and the origin. (a = 21/10, 3, 5, 10, 100 )

This also indicates that 2 is a boundary.

What happens when a is negative?
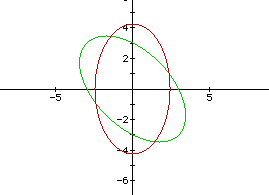
Using the coefficents a = 0, -1, -2 and -3 , we see that the original graphs are reflected across the x or y axis ( or rotated 90 degrees) but hold the same characteristics.

Commonalities between the graphs:

They all have common intersection points at the x and y intercepts (+ or - 3). This can be supported by substituting x = 0 or y = 0 into the general equation.
They all have symmetry about the y = x and the y = - x lines.
The boundaries are 0 and -2.

In closing, I wanted to know what happens to the boundaries when the radius is changed. Using the equations:

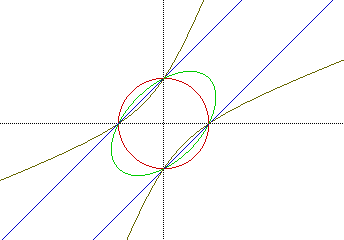
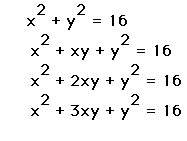
we find that the boundaries are still 0, 2, and -2. The radius only changes the x and y intercept. All values of c for:

will produce:

a circle when a = 0.
an ellipse when 0 < a < 2.
two straight lines when a = 2 or -2.
a hyperbola when a > 2 or a < -2

Return to Kelli's Class Page