Andy Norton

Department of Mathematics Education

University of Georgia

*see other examples

Spreadsheets Using the TI Calculator and CBL


The following experiment was conducted using the TI-83 (Texas Instruments) calculator and the CBL (Calculator-Based Laboratory) system. We measure the cooling of water with the temperature probe for the CBL. This data is read every minute and fed into the TI-83 calculator. The calculator, then, graphs the data on the X-Y plane.

Once all data has been read and graphed, we can use the calculator to find best-fitting curves. We will try a linear, quadratic and exponential fit. To learn more about the TI calculators and CBL capabilities and programs, Click Here.

After uploading the data from the TI to a CPU (using the TI-graph link), we can plot the time and temperature data on a spreadsheet. We can graph it on the spreadsheet, as well as graphing the best-fitting curves. Then we will find the error in our analysis by the least squares method. This will also be done in the spreadsheet.

Listed below are the data for the cooling of boiling (or nearly so) water over a 30 minute period, taken every minute. The left column displays time from the start of the experiment. The temperature at each time is given on the right.

Time (in Seconds) Temperature (in Celcius)
0 89.23
60 89.23
120 85.42
180 82.53
240 79.91
300 77.67
360 75.61
420 73.67
480 71.75
540 70.2
600 68.92
660 67.41
720 66.02
780 64.67
840 63.48
900 62.21
960 61.26
1020 60.05
1080 58.97
1140 58.14
1200 57.26
1260 56.46
1320 55.52
1380 54.68
1440 53.92
1500 53.11
1560 52.37
1620 51.79
1680 50.92
1740 50.43
1800 49.86


Now, we return to our TI-83 calculator to assist in finding a best-fit curve. We will consider three types: linear, quadratic and exponential.

In each case, X represents time and Y represents temperature, so we have temperature as a function of time. Also, in each case we must find the constants, 'a','b' and 'c', that best fit our data.

Without the calculator, we might guess 'b' will be the initial temperature of the water, for the first equation, since Y = b at t=0. Likewise 'c' will be the initial temperature of the water in the second equation. Then 'a', in the first equation, and 'a' and 'b', in the second equation will describe how fast the water is cooling. We could find these values by plugging data into these equations and solving for 'a', 'b' and 'c', but the caluculator should be faster and more accurate, since it will consider all data points.

For the linear fit, the TI-83 chooses, a = -.02 and b = 83.11.

For the quadratic, we have a = 9.33 x E (-6), b = -.04 and c = 89.02.

Let's look at these graphs versus our data:


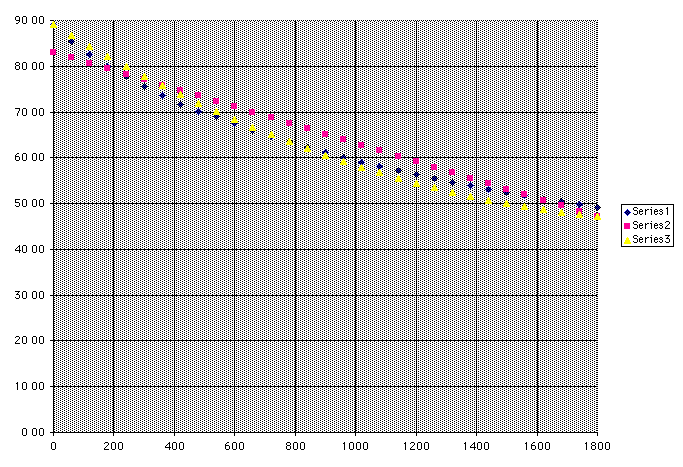
We see the real data in blue. The pink line is the TI's linear fit. The yellow line is the TI's quadratic fit. Note that the quadratic fit is pretty convincing. In fact, we can measure just how convincing it is.

The TI would not give a good exponential regression line because the 'b' value needed is too close to 1 (the TI approximated this value to 1 which, you will note, genterates a straight line in our exponential equation).

However, by using the least squares method on our spreadsheet, we can fing a good exponential fit to our data:




We see that the exponential fit is also convincing. We can use the least squares method to determine which, quadratic or exponential, is the more fitting fit. Unfortunately, we find that the quadratic fits the given data a little more accurately (4.09 versus 3.13). This may be because we have an inaccurate room temperate reading (used in the exponential but not the quatratic equation). Also, remember that the TI, more nimble than human, calculated the constants for the quadratic. We calculated the exponential constants by hand on the spreadsheet.

It is important to realize that the exponential fit is actually more appropriate. To see this, consider the temperature as hours, days or years pass. The exponential equation will reveal a tendency toward room temperature. The quadratic will tend toward a more Hell-ish one.

To see the spreadsheet with all this data and graphs, Click Here.

We can use the spreasheet with our exponential equation to predict the water temperature at unplotted times:

After 45 minutes, we have Temperate = 36.71 degrees Celcius.
After an hour, Temperature = 31.06 degrees Celcius.
After one day, we are at room temperature, as expected.

So, we were able to use the TI and CBL technology to gather data for us, efficiently and accurately. The TI was also able to offer some possible regression fits to our data and plot them. Then, the spreadsheet helped to find a suitable exponential fit with minimal error. It provided clear graphs for comparisson, and let us predict temperatures at times not recorded. This is just one example of how technology can aid in data experiments.