University of Georgia
*see other examples
Game Day!
The football rules in college football were changed a few years
ago have made the uprights 5 feet narrower than previously. Many
game commentators have harped about how much harder it is to kick
field goals from the hash marks.
Assume the field goal is attempted from the hash marks. At what
yard marker does the kicker have maximum angle to the two uprights.
Is there any merit to some commentators argument to take a penalty
in order to have a "better angle" on the field goal
kick?
Our football delima is one of subtending angles.
We turn to Dr. Math for a definition of this mathematical term:
If you think of the side opposite say angle A in a
triangle, then that
side 'SUBTENDS' angle A. The word is most commonly used for the
chord
of a circle, SUBTENDING an angle at the circumference or at the
centre
of the circle. You can also think of the arc of a circle subtending
an
angle at the centre or at the circumference. The angle subtended
is
'opposite' the chord or arc.
-Doctor Anthony, The Math Forum
Check out our web site! http://forum.swarthmore.edu/dr.math/
You can create some subtending angles of a fixed
segment by clicking on the following GSP script file: Subtend.gss
Now, let's look at a GSP file which illustrates
the problem. Click on the picture below to see an animation of
kicking angles at different points on the right hash-line.
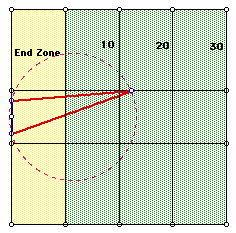
In the animation, we have a measure of the "kicking angle."
Here, when we use the term kicking angle, we refer to the angle
that subtends the width of the field goal from any fixed point
along the right hash-line. Notice where this angle is maximized...
In the subtend.gss script we see that the locus
of verteces for a fixed angle subtending a fixed segment is a
circle. In other words, if a segment defines a cord of a circle,
then any point on the circle outside the arc formed by that cord
subtends that cord (or segment) at a fixed angle. Realizing this
statement is a little complicated, let's, once again, turn to
an illustration...

By clicking this picture, you can go to a GSP file which will
allow you to move point C and observe that the angles on the circle
subtending AB remain constant. Also, notice that, for bigger circles,
the angles are smaller and visa versa. So, in order to maximize
the kicking angle, we want to minimize the size of the circle.
In order to understand this, consider the equilateral triangle
ABC. We can form a right triangle ADC by dividing ABC in half,
thus dividing the subtending angle of AB in half. We know that:
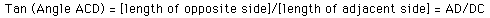
Clearly, this ratio is getting smaller as C moves further out.
In fact, the limit as C moves away from AB is 0, and we know that
the Tangent of an angle is zero when the angle is zero.
Moving on, let us return to our football problem...
At what distance on the right hash-line, is our angle maximized?
This point, as discussed, will be the point on the right hash-line
which defines, with the segment formed by the field goal, the
smallest circle. Since the circle bounded by the hash-marks will
be smaller than those that extend beyond it, and since the circle
must include a point on the hash-marks, the smallest cirlce will
have the hash-line as a tangent line.
The following script finds the center of the previously described
circle for any field goal and hash-mark width. By drawing a perpendicular
form this center to the hash-line, we obtain and measure the maximal
kicking angle...
Kicking Angle.gss
By using this script and the following College
Football regulations:
a) The right hash mark is 5 yards (or 15 feet) from the center
of the field.
b) The new regulation field goal width is 18.5 feet.
...we can now do a GSP construction to find this maximal kicking
angle. We find that the maximal kicking vertex is about 3 yards
from the back of the end zone and the maximal angle is about 26
degrees. Unfortunately, kickers cannot cannot kick within the
endzone. In fact, they kick 7 yards behind the line of scrimage.
So the best kicking angle, on the hash-marks, is at the 7 yard
line.
Note, then, that there is no advantage of taking a penalty for
a "better angle." The best angle is found in the closest
spot.
Link to ESPN
College Football


