Learning from and experimenting with Parametric Equations

Suppose that x and y are both given as continuous functions of a third variable t (called a parameter) by the equations, x = f(t) & y = g(t) (called parametric equations). Each value of t determines a point (x,y), which we can plot in a coordinate plane. As t varies, the point (x,y) = (f(t),g(t)) varies and traces out a curve C. If we interpret t as time and (x,y) = (f(t),g(t)) as the position of a particle at time t, then we can imagine the particle moving along the curve C.

What is the curve represented by the parametric equations x = cos(t) and y = sin(t)?

 A circle is created as t is varies through the range from .

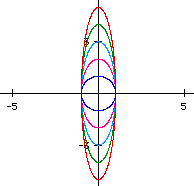
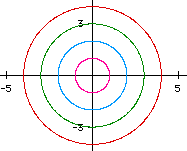
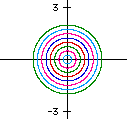
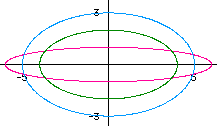
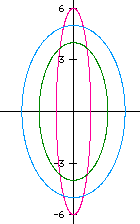
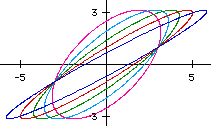
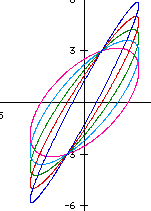
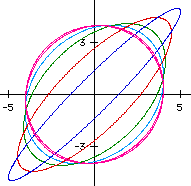
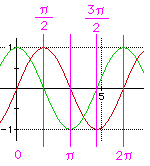
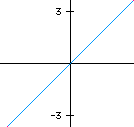(Diagram below right) The sine and cosine curves give us the information concerning why a circle is formed as t varies. Notice that if t = 0, then the value of cosine = 1, and the value of sine = 0, (1,0). When t = pi/2 the ordered pair is (0,1), at t = pi it is (-1,0), at t = 3pi/2 it is (0,-1) and then finally when t returns to 2pi with a value of (1,0).

 

 

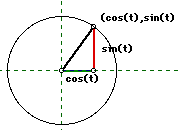What happens when we manipulate the values of a and b

in the parametric equations x = a cos(t) and y = b sin(t)?

Holding a constant at 1, and manipulating b we find that as b increases the y values expand from the x axis, and as b approached zero the y values would compress to the x axis.

 Holding b constant at 1, and manipulating a we find that as a increases the x values expand from the y axis, and as a approached zero the x values would compress to the x axis.

 

 

Manipulating a and b simultaneously with both values increasing but both being equal creates concentric circles that expand from the origin.

 Manipulating a and b simultaneously with both values decreasing but both being equal creates concentric circles that compress to the origin.

 

 

A horizontal oval is created when a is greater than b.

An vertical oval is created when b is greater than a.

 

 

What happens when we manipulate the values of a, b, g, and h

in the parametric equations x = a cos(t) + g sin(t) and y = b sin(t) + h cos(t)?

When a = h and b = g. The line y = x is formed
  When a is increased and g = h = 3 and b = 1.

 

 
 When b is increased and g = h = 3 and a = 1.

 When h and g decreased and a = b is held constant we approach the original circle.

 

 

The End!!