EMT 668--Assignment 1

Exploring the Graphs of Two
Distance Equations

The two distance equations being explored are:

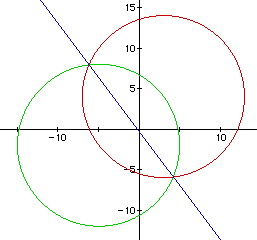
Throughout the rest of this exploration, I will refer to the two distance equations as Distance1 and Distance2, as stated above.

A. Figure 1 below shows two circles, one for Distance1 = 10 (in red) and one for
Distance2 = 10 (in green). Notice that the center of the red circle is at (3,4) and the center of the green circle is at (-5,-2), which corresponds to their respective equations.

Figure 1

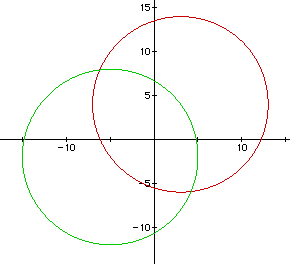
B. Now we will explore the sum Distance1 + Distance2 = C, where C is some positive integer. Figure 2 shows the graph of Distance1 + Distance2 = 12 (in blue). By adding the distance equations together an ellipse is formed. Notice that the foci of the ellipse are at the centers of the two cirlces.

Figure 2

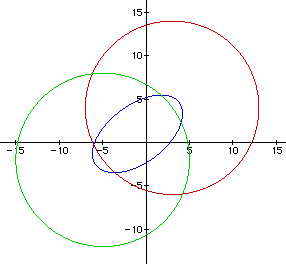
Figure 3 shows the graph of Distance1 + Distance2 = 20 (in purple). As the value of C went from 12 in Figure 2 to 20 in Figure 3, the ellipse grew larger. Also, when C=20 the ellipse that is formed crosses through the two points of intersection between the two distance equations.

Figure 3

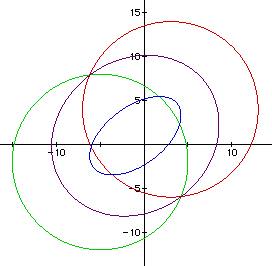
Figure 4 shows the graph of Distance1 + Distance2 = 30 (in olive). Notice that the ellipse is continueing to get larger. This ellipse is also tangent to the outside of the two circles formed from the two distance equations.

Figure 4

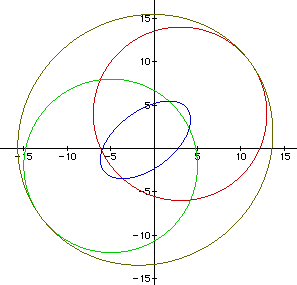
Figure 5 is when Distance1 + Distance2 = 31 (in purple). This shows that when C becomes larger than 30, the ellipses that are formed completely engulfs the two circles formed in Figure 1.

Figure 5

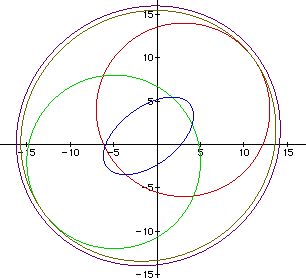
Figure 6 shows the graph:

(in purple).

The ellipse has now become very narrow now that C is approaching 10. As can be seen in
Figure 7, the closer C comes to 10, the more like a straight line the ellipse looks.

Figure 6

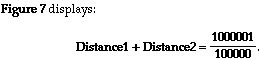
Notice how much this figure needed to be enlarged in order to see that the ellipse was not a straight line.

Figure 7

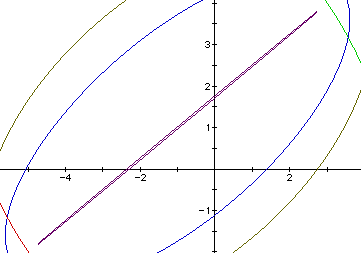
C. Figures 8 through 13 are an exploration of Distance1*Distance2 = C, for some integer C.
Figure 8 is the graph of Distance1*Distance2 = 24 (in blue). For C values less than 24, the blue objects become smaller and smaller.

Figure 8

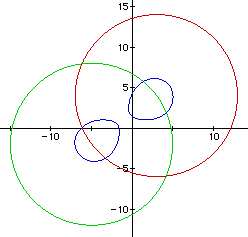
Figure 9 is when C = 25. The two objects are now touching.

Figure 9

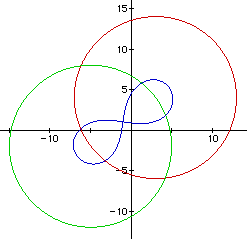
Figure 10 is when C = 27. As the value of C is increased, the two objects become one object and form an ellipse. The larger the value of C gets, the larger the ellipses become.

Figure 10

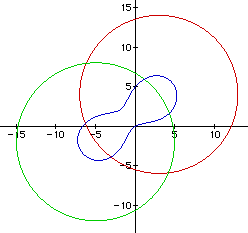
Figure 11 is for C = 100 (in blue), this is a special case ellipse because it passes through the two points of intersection of the two circles from Figure 1.

Figure 11

Figure 12 is for C = 200, this forms another ellipse which is also a special case ellipse because it is tangent to the two circles.

Figure 12

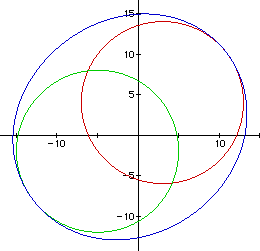
Now as the value of C continues to get larger the ellipse becomes larger and surrounds both circles. This is displayed in Figure 13 with C = 250.

Figure 13

D. All of the figures from here to the end are from further explorations of the two distance equations. These explorations are Distance1 / Distance2 = C and
Distance2 / Distance1 = C, for some C. C does not have to be an integer.

Figure 14 displays Distance1 / Distance2 = 2 (in blue). Notice that the circle that is formed is tangent to the larger green circle.
What would the graph look like if we had Distance2 / Distance1 = 2 ?

Figure 14

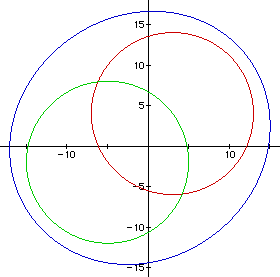
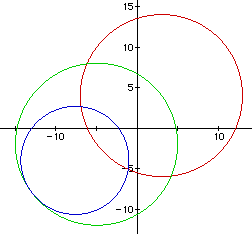
Figure 15 shows the answer to the questioned raised in Figure 14. Now the new circle formed is tangent to the larger red circle. Is this what you had predicted?

Figure 15

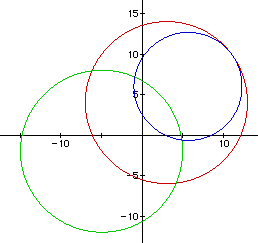
Now as C increases, what do you expect to happen to the circle? Figure 16 shows the graph of Distance2 / Distance1 = 5. This forms a circle that is inside of the red circle. It is not shown here, however, Distance1 / Distance2 = 5 will just be the reflection of Figure 16 through the origin. This will thus form a circle that is inside of the green circle.

Figure 16

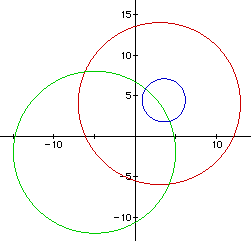
Now when C < 2 , what do you expect to happen to the circle? As the value of C decreases below 2, the circle that is formed gets increasing larger than the red or green circle. Figure 17 displays the graph Distance2 / Distance1 = 8/5 or 1.6. Once again, Distance1 / Distance2 = 8/5 or 1.6 will just be the reflection of Figure 17 through the origin.

Figure 17

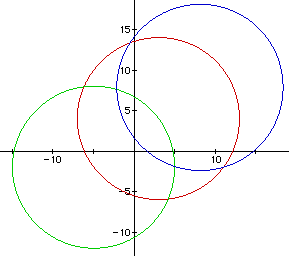
There is one more exploration that is of interest. What happens when Distance1 / Distance2 = 1 or Distance2 / Distance1 = 1 ? This is intersting because you get a straight line. As the value of C got closer and closer to 1 the the circles continued to get larger and larger until at 1 they combine to form a straight line. If C drops below 1, nothing really new is formed. What happens is the graphs that we have just dicussed for Distance2 / Distance1 = C will become the ones that we discussed for Distance1 / Distance2 = C and vice-versa. This can be seen with doing some simple math on the equation Distance1 / Distance2 = C or Distance2 / Distance1 = C. Figure 18 is a graph of the straight line that forms when either Distance2 / Distance1 = 1 or Distance1 / Distance2 = 1.