---

Nine Point Circles

---

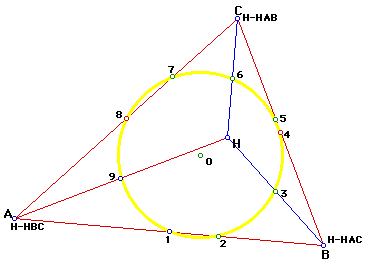
Which of the four triangles that we have been talking about do you think this nine point circle was constructed from? In all realty, the picture above is that of all four nine point circles, one for each the four triangles, triangles ABC, HAB, HAC, and HBC. Yes, all four triangles have the same ninepoint circle. The nine points on the circle are numbered so that they can be put into the nine categories listed previously describing what each point represented. Below is that list repeated four times identifying which category each point falls in for the four different triangles being discussed.

For triangle ABC:

• The midpoint of segment AB => 1
• The midpoint of segment AC => 8
• The midpoint of segment BC => 4
• The midpoint of segment HA => 9
• The midpoint of segment HB => 3
• The midpoint of segment HC => 6
• The point of intersection between line AB and the altitude passing through point C => 2
• The point of intersection between line AC and the altitude passing through point B => 7
• The point of intersection between line BC and the altitude passing through point A => 5

For triangle HAB:

• The midpoint of segment AB => 1
• The midpoint of segment HB => 3
• The midpoint of segment HA => 9
• The midpoint of segment HH-HAB => 6
• The midpoint of segment BH-HAB => 4
• The midpoint of segment AH-HAB => 8
• The point of intersection between line AB and the altitude passing through point H => 2
• The point of intersection between line HA and the altitude passing through point B => 5
• The point of intersection between line HB and the altitude passing through point A => 7

For triangle HAC:

• The midpoint of segment HA => 9
• The midpoint of segment AC => 8
• The midpoint of segment HC => 6
• The midpoint of segment AH-HAC => 1
• The midpoint of segment HH-HAC => 3
• The midpoint of segment CH-HAC => 4
• The point of intersection between line HA and the altitude passing through point C => 5
• The point of intersection between line AC and the altitude passing through point H => 7
• The point of intersection between line HC and the altitude passing through point A => 2

For triangle HBC:

• The midpoint of segment HB => 3
• The midpoint of segment BC => 4
• The midpoint of segment HC => 6
• The midpoint of segment BH-HBC => 1
• The midpoint of segment HH-HBC => 9
• The midpoint of segment CH-HBC => 8
• The point of intersection between line HB and the altitude passing through point C => 7
• The point of intersection between line HC and the altitude passing through point B => 2
• The point of intersection between line BC and the altitude passing through point H => 5

All these lists were defined right from the image above and and the definitions of altitudes and orthocenters. A main reason behind why all four triangles have the same nine point circles lies in the fact that two of the three sides of the original triangle ABC become altitudes of triangles HAB, HAC, and HBC.

Return to Altitudes and Orthocenters