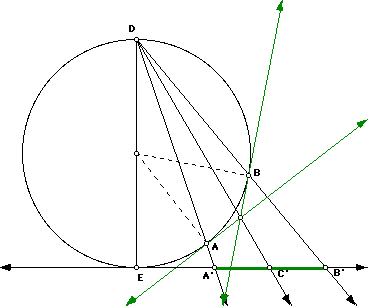
PROBLEM: Intersection of Lines through Points of Tangency |
Looking at the drawing below, prove that A'C' is congruent to C'B'.

The solution put forth here is an algebraic means of solving the problem. The Law of Sines and Law of Cosines are used often in this solution.
Let![]() ,
, ![]() and
and ![]() .
.
Thus,
If C'B' = A'C',
then
.
Since, ![]() and
and![]() ,
, ![]() .
.
Therefore,
simplifies to
.
Now defining each term in this last expression we get,
Thus,
becomes
and after simplifying one is left with A'C' = C'B'.
Therefore, A'C' is congruent to C'B'.
Questions, Comments or
Suggestions
©1998 by Luke Rapley