

Philippa M. Rhodes
Four dogs, A, B, C, and D are located at the vertices of a square. They start to run at the same time and at the same speed. A runs toward B, B runs toward C, C runs toward D, and D runs toward A.
Eventually they all meet in the center of the square. Why?
What are the paths followed by the four dogs?
Thus far, I have usedGeometer's Sketchpad. to help draw the paths of the dawgs. The vertices of the square are the starting points for the four dawgs. Translate each point by a small distance along the side towards the particular point.
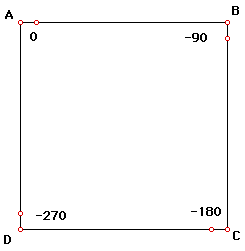
The next point should be the same distance but at a marked angle:
A' should be translated the small distance by angle BA'B', ect.
First time:
A was translated 0 degrees
B -90 deg
C -180 deg
D - 270 deg
The next time each point is translated, add the angle to the angle from the previous time.
2nd time:
A -4.125 deg, B -94.125 deg, etc.
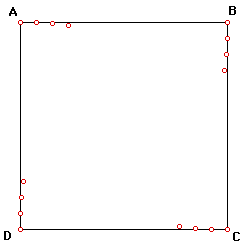

I think that these paths are headed in the right directions, but at the rate of this curve, they will not meet in the middle. I may have to reconsider the angle that I am using to translate the points, or I may need to try a completely different process. I can not say that I have learned anything that I feel is new to me from doing this problem so far. I have enjoyed trying it; so, I do not feel that I have wasted any time. I know that other people have solved this problem, but I am going to keep modifying what I have done until I find a solution. If I do reach a point of of ultimate frustration, I will look at another solution.