
Bill Tankersley's EMT 668 Page
Final Project - Part 2
The assignment for Part 2 of the Final Project is to select an item
from one of the assignments that was not written up previously and submit
a write-up on that item. The write-up should be representative of "best
work" in the course.
I chose problem 5 from assignment 4, which is the following:
Use GSP to construct G, H, C, and I for the same triangle. What relationships
can you find among G, H, C, and I, or subsets of them? Explore for many
shapes of triangles:
A quick review: G = Centroid, H = Orthocenter, C = Circumcenter, and I =
Incenter.
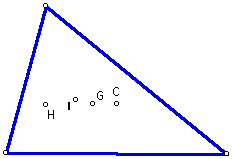
The triangle above is shown with each of the 4 triangle centers, G,
H, C, and I.
Click here to download the GSP file of the drawing
above.
To begin an exploration of possible relationships, let's start by considering
the following 3 classifications of triangles: Acute, Right, and Obtuse.
The following observations were made after repeatedly changing the shape
and size of triangle ABC and analyzing the locations of H, G, C, and I.
Observations
The reader is invited to download the GSP file and investigate each
of the following claims:
1.) H, G, C, are always collinear. This line is known as the Euler Line.
2.) H is always nearest the angle with the largest degree measure.
3.) If triangle ABC is equilateral, then the four triangle centers become
the same point.
4.) If triangle ABC is isosceles, then I is also on the Euler line.
5.) If triangle ABC is a right triangle, then H is the vertex of the right
angle and C is on the hypotenuse. The Euler line becomes the median from
the right angle to the opposite side.
6.) G and I always remain on the interior of the triangle, while H and C
will be located on the exterior of the triangle if ABC is obtuse.
7.) G is always located between H and C.
8.) I is always between G and H.
9.) For obtuse angles, C exits the triangle interior through the longest
side, while H always exits the triangle interior through the vertex of the
angle with the largest measure.
10.) HG = 2GC for all triangles.
End of Part 2


