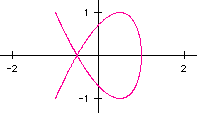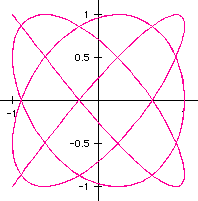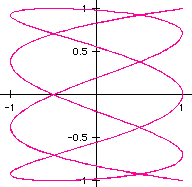Bill Tankersley's EMT 668 Page
Write-up 10
Assignment 10 - Problem 2
Parametric Curves
Problem: For various values of a and b, investigate:
x = cos(at)
y = sin(bt)
for values of t between and including 0 to 2 pi.
To begin the investigation, let's get a picture of the graphs of x= cos(t)
and y= cos(t):
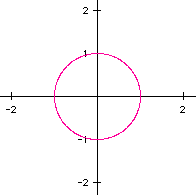
What we see here is a closed curve with radius 1 commonly referred to
as the "Unit Circle". This stands to reason, since we are letting
t take on values from 0 to 2 pi.
For this investigation, I plan on letting a and b take on various values
from 1 to 10, and then forming some sort of conjecture. As long as a and
b are equal, the graph will always be the same as the graph above, which
is a circle of radius 1. What we need to do is let a and be take on different
values.
Now, let's see what happens when a=1 and b=2:
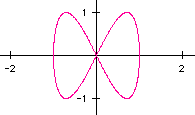
It looks like we got a nice "bowtie" effect. Let's try reversing
a and b, that is, letting a=2 and b=1:
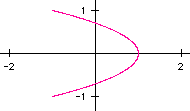
This graph resembles a sideways parabola. Next, let's try a=1 and b=3:
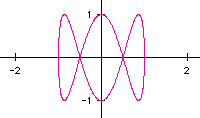
Now let's look at more of these graphs as we vary the values of a and
b:
1) a=2, b=3:
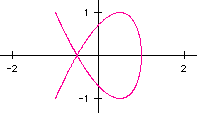
2) a=3, b=2:
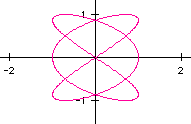
3) a=4, b=9:
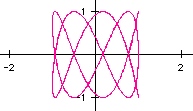
4)a=5, b=8:
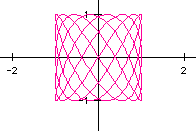
A point of interest I chose to investigate here is the fact that when
a is even and b is odd, part the graph is left open at some point. For example,
notice the graphs above for a=2,b=1 as well as a=2,b=3. Both of these graphs
do not fully reconnect. Also, the graph of a=4, b=9 above has two endpoints
that do not reconnect, although they are not quite as obvious as the others
mentioned. Let's investigate and see what happens as we continue to let
a be an even number and b be an odd number:
5) a=6, b=7
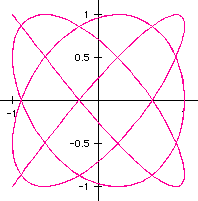
It looks like our conjecture holds again. We let a be even and b be
odd, and we got another graph that is not fully connected. Notice the two
endpoints on the left side of the graph that do not reconnect to the rest
of the graph. Let's look at two more cases with a even and b odd.
6) a=8, b=3
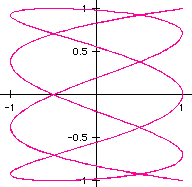
7) a=4, b=7
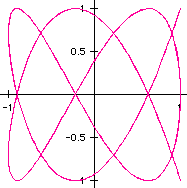
The conjecture still holds. When a is an even value and b is an odd value,
the graph will have two parts somewhere that are unconnected. Another avenue
to investigate would be to see if we could determine on which side of the
graph the unconnected parts are based on the equation. Judging from the
graphs above, I believe that if a and b differ by exactly one number, then
the unconnected parts of the graph will lie on the left side of the graph.
If a and b differ by more than one number, then the unconnected parts will
lie on the right side of the graph. More cases would need to be tested,
but I feel that there is reasonable cause to believe the conjecture.
Return to Bill Tankersley's EMT 668 Page